Forum de Mathématiques: Maths-Forum

Bonjour, Je dois montrer par le théoreme des accroissements finis que pour tout x appartenant à [0,1] on a : 0 <= sin(x) <= x J'ai utilité |cos(x)|<=1 ce qui me permet d'écrire : |sin(x)-sin(0)|<=|x-0| et donc |sin(x)|<=x ce qui revient à -x <= sin(x) <= x Je ne comprends pas comment avoir le 0 à ga...

Bonjour,

soit le système d'équations AX=B

Je sais que si det(A) est non nul alors le système admet une unique solution.
Mais que peut-on dire du cas où det(A)=0 ?

Merci

je n'ai pas compris...

Bonjour, Je n'arrive pas à comprendre la limite de cette fonction : f(x)=0.5*x+0.5-0.5*\sqrt(x^2-2*x+1) pour moi la racine est équivalente à x en plus l'infini donc les 0.5x se simplifient et il ne reste que 0.5. Or a la calculatrice on voit que la limite est 1. Je ne vois pas commen...

Bonjour, pouvez vous m'aider à résoudre cette équation :



avec a0(t)=D

je ne sais pas comment démarrer ..

c'est bon je viens de voir mon erreur ..

En fait j'ai un problème j'ai fait le calcul avec le polynôme :


alors que

ça ne donne pas une différence inférieure à 10^-5...

ok merci !

Bonjour, Je dois montrer que : |cos(x)-1+x^2/2-x^4/4!| \le x^6/6! Pour cela je me sers du théorème de Taylor Lagrange, le reste est R(x) = cos(c)*x^6/6 Peut-on dire directement que |cos(x)-1+x^2/2-x^4/4!| \le cos(c)*x^6/6! ? Puis majorer le cosinus par 1? Ensu...

Ok je crois que j'ai compris effectivement ce n'est pas le meilleur exemple pour comprendre la composition ...

Désolé mais je comprends pas.

Si je fais le DL de sin(y) en 0 à l'ordre 3 j'ai :
sin(y)=y-y^3/3! + o(y^3)

Si je remplace y par x^2 j'obtiens sin(x^2)=x^2-x^6/3! + o(x^6)

Je n'arrive pas à comprendre pourquoi c'est juste car je crois que je n'ai pas compris comment faire la composition de DL.

c'est à dire que je fais le DL de sin(x) à l'ordre 3 et je remplace x par x^2 ?

Il s'agit de non ?
Moi je cherche

bonjour,

Je dois calculer le DL de f(x)=sin(x^2) en passant par le développement limité de g(y)=sin(y).

Est-ce qu'il faut utiliser la composition de DL? J'ai du mal à comprendre la méthode.

Ok merci!

Bonjour,

On me demande d'écrire la formule de Taylor Lagrange pour la fonction tan(x) en 0 à l'ordre 4.
Y-a-t-il un moyen plus rapide que de calculer toutes les dérivées jusqu'à l'ordre 4? Ca me parait fastidieux !

bonjour,

soit la suite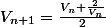

et V0=2

Je ne vois pas du tout quoi faire je n'arrive meme pas a montrer si elle est croissante ou décroissante. J'ai essayé Vn+1-Vn et Vn+1/Vn mais ça ne donne rien

je ne vois pas comment montrer qu'elle est majorée par 2

Bonjour, je dois étudier la suite : U_{n+1}=1+\frac{U_n^2}{4} avec U_0 \ge 0 J'ai essayer de calculer Un+1 - Un et je me retrouve avec un polynome de Un de degré 2 qui ne s'annule quand 1 seul point Un=2 Est ce que je peut conclure que la suite est strictement croissante si U0 différent de 0 est sta...

merci !