ce qui me semble être la bonne réponse merci pour votre aide.
33 résultats trouvés
Revenir à la recherche avancée
Re: carré et cube d'une somme à n éléments
J'obtiens :
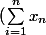^3=\sum_{i=1}^n x_i^3+3\sum_{i=1}^{n-1}\sum_{j=i+1}^n (x_i^2x_j+x_j^2x_i)+6\sum_{i=1}^{n-2}\sum_{j=i+1}^{n-1}\sum_{k=j+1}^n x_ix_jx_k)
ce qui me semble être la bonne réponse merci pour votre aide.
ce qui me semble être la bonne réponse merci pour votre aide.
- 09 Juil 2018, 19:01
- Forum: ✯✎ Supérieur
- Sujet: carré et cube d'une somme à n éléments
- Réponses: 13
- Vues: 7874
Re: carré et cube d'une somme à n éléments
D'accord merci beaucoup à vous.
- 09 Juil 2018, 16:07
- Forum: ✯✎ Supérieur
- Sujet: carré et cube d'une somme à n éléments
- Réponses: 13
- Vues: 7874
Re: carré et cube d'une somme à n éléments
Alors je trouve un résultat de cette façon faux mais proche du coup je me demande où j'ai pu me tromper si vous pouvez m'indiquer merci. A=(\sum_{i=1}^n x_i)^3=\sum_{1\le i,j,k\le n} x_ix_jx_k=\sum_{1\le i,j,k\le n, i=j} x_ix_jx_k+\sum_{1\le i,j,k\le n, i\neq j} x_ix_jx_k A=\sum_{1\le i,k\le...
- 09 Juil 2018, 12:57
- Forum: ✯✎ Supérieur
- Sujet: carré et cube d'une somme à n éléments
- Réponses: 13
- Vues: 7874
Re: carré et cube d'une somme à n éléments
D'accord merci beaucoup pour votre aide, donc pour le cube on peut faire de la même manière je suppose, je vais tester.
- 09 Juil 2018, 11:04
- Forum: ✯✎ Supérieur
- Sujet: carré et cube d'une somme à n éléments
- Réponses: 13
- Vues: 7874
Re: carré et cube d'une somme à n éléments
Effectivement merci à vous deux, mais du coup comment je "fais un travail analogue" pour le cube ? compliqué pour moi tout ça ... Du coup c'est réellement par récurrence qu'il faut le démontrer ?
- 08 Juil 2018, 22:21
- Forum: ✯✎ Supérieur
- Sujet: carré et cube d'une somme à n éléments
- Réponses: 13
- Vues: 7874
carré et cube d'une somme à n éléments
Bonjour, je me trouve dans l'incapacité de prouver rigoureusement (je vois que ça marche) que 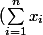^2=\sum_{i=1}^n x_i^2+2\sum_{i=1}^{n-1}{\sum_{j=i+1}^n x_ix_j}) ce qui me bloque pour la suite ...
ce qui me bloque pour la suite ...
Je vous remercie de votre aide, bonne soirée.
Je vous remercie de votre aide, bonne soirée.
- 08 Juil 2018, 22:05
- Forum: ✯✎ Supérieur
- Sujet: carré et cube d'une somme à n éléments
- Réponses: 13
- Vues: 7874
Re: fonction de densité d'une loi normale
Et bien merci beaucoup pour ton aide je n'avais pas pensé à cette approche, merci.
- 20 Mai 2018, 11:27
- Forum: ✎✎ Lycée
- Sujet: fonction de densité d'une loi normale
- Réponses: 2
- Vues: 429
fonction de densité d'une loi normale
Bonjour, je n'arrive pas à trouver comment obtenir la fonction de densité d'une loi normale générale en partant de celle d'une loi normale centrée réduite : soit Z une variable aléatoire dans \mathbb{R} tel que Z\sim\mathcal{N}(0;1) , soit X une variable aléatoire \mathbb{R} vérifiant Z=\fra...
- 19 Mai 2018, 21:43
- Forum: ✎✎ Lycée
- Sujet: fonction de densité d'une loi normale
- Réponses: 2
- Vues: 429
Re: valeurs approchées de e
Effectivement merci, j'avais dérivé 0 . . .
- 27 Oct 2017, 17:24
- Forum: ✎✎ Lycée
- Sujet: valeurs approchées de e
- Réponses: 8
- Vues: 480
Re: PROBLÈME DE MATHS SECONDE-Fonctions
Tu es bloqué à partir d'où ?
- 26 Oct 2017, 15:13
- Forum: ✎✎ Lycée
- Sujet: PROBLÈME DE MATHS SECONDE-Fonctions
- Réponses: 25
- Vues: 2233
Re: valeurs approchées de e
J'aboutis à =-e^{-x}\left(\sum_{k=0}^n \frac{x^k(1-\frac{k}{x})}{k!}\right))
Je pense que j'ai dû loupé un truc ça me semble bizarre.
Je pense que j'ai dû loupé un truc ça me semble bizarre.
- 25 Oct 2017, 15:48
- Forum: ✎✎ Lycée
- Sujet: valeurs approchées de e
- Réponses: 8
- Vues: 480
Re: valeurs approchées de e
Puisque f_n(x)=\frac{x^n}{n!}e^{-x} f_n(0)=0 Et j'ai montré ensuite que f_n est croissante de 0 jusqu'à n pour n \ge 1 Du coup f_n(x)\ge 0 pour x\in [0;1] et n\ge 1 Donc son intégrale sur [0;1] est aussi positive et du coup u_n\ge 0 J'ai fait un tableau de variations mais je ...
- 25 Oct 2017, 14:47
- Forum: ✎✎ Lycée
- Sujet: valeurs approchées de e
- Réponses: 8
- Vues: 480
Re: valeurs approchées de e
Merci effectivement j'ai ajouter c'est stupide, sinon comme autre information j'ai 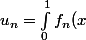\, \mathrm{d}x)
Donc il faut que je montre que est positive sur [0;1] du coup.
est positive sur [0;1] du coup.
Donc il faut que je montre que
- 25 Oct 2017, 14:24
- Forum: ✎✎ Lycée
- Sujet: valeurs approchées de e
- Réponses: 8
- Vues: 480
Re: valeurs approchées de e
Je pense avoir trouver avec une démonstration par récurrence où l'hérédité est : u_n \ge 0 \Leftrightarrow 1-\left(\sum_{k=0}^n \frac{1}{k!}\right)e^{-1}\ge 0 \Leftrightarrow 1-\left(\sum_{k=0}^{n+1} \frac{1}{k!}\right)e^{-1}\ge \frac{1}{(n+1)!}e^{-1} \Leftrightarrow u_{n+1}\...
- 25 Oct 2017, 13:16
- Forum: ✎✎ Lycée
- Sujet: valeurs approchées de e
- Réponses: 8
- Vues: 480
valeurs approchées de e
Bonjour, dans un exercice guidé visant à déterminer e sous sa forme e=\lim_{n \to +\infty}\left(\sum_{k=0}^n \frac{1}{k!}\right) Je me retrouve bloqué ici : \forall n\ge1 I_n(a)=1-\left(\sum_{k=0}^n\frac{a^k}{k!}\right)e^{-a} On prend a=1 alors \forall n\ge 0 On pose u_n=I_n&...
- 25 Oct 2017, 12:50
- Forum: ✎✎ Lycée
- Sujet: valeurs approchées de e
- Réponses: 8
- Vues: 480
Re: fonctions
Tu peux utiliser une identité remarquable sur 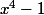
Re: nombres complexes i^i
Je me posais juste la question et au moins maintenant je sais pourquoi c'est plus compliqué que ce que je pensais merci beaucoup.
- 24 Oct 2017, 22:12
- Forum: ⚔ Défis et énigmes
- Sujet: nombres complexes i^i
- Réponses: 17
- Vues: 888
Re: nombres complexes i^i
Je ne sais pas justement. 

- 24 Oct 2017, 21:55
- Forum: ⚔ Défis et énigmes
- Sujet: nombres complexes i^i
- Réponses: 17
- Vues: 888
Re: nombres complexes i^i
En généralisant pour z et z' deux complexes je trouve : z^{z'}=(|z|e^{iarg(z)})^{z'}=|z|^{Re(z')+iIm(z')}(e^{iarg(z)})^{Re(z')+iIm(z')} Soit z^{z'}=|z|^{Re(z')}|z|^{iIm(z')}e^{iarg(...
- 24 Oct 2017, 21:39
- Forum: ⚔ Défis et énigmes
- Sujet: nombres complexes i^i
- Réponses: 17
- Vues: 888
Re: nombres complexes i^i
Mon résultat est-il correct ce coup-ci ?
- 24 Oct 2017, 19:52
- Forum: ⚔ Défis et énigmes
- Sujet: nombres complexes i^i
- Réponses: 17
- Vues: 888
- 33 résultats trouvés - Page 1 sur 2 • 1, 2
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
