243 résultats trouvés
Revenir à la recherche avancée
Bonjour, Afin de déterminer une matrice dans la base canonique de \mathbb{C}^3 , à partir de f, un endomorphisme de \mathbb{C}^3 , j'ai trouvé que : f(1,0,0) = (1,-m,0) f(0,1,0) = (0,1,-m) f(0,0,1) = (-m,0,1) Maintenant, je dois chercher les coefficients a_{ij} en chaque triplet. Le problème, c'est...
- 05 Mai 2012, 17:37
- Forum: ✯✎ Supérieur
- Sujet: Coefficients matrice
- Réponses: 2
- Vues: 636
Un vrai sujet cette fois: :ptdr: A,B des matrices carrés d'ordres n. c,d \in R- {0} telles que: AB + cA+dB=0. Montrer qu'on a AB = BA Ton hypothèse peut s'écrire (A+dId)(B+cId)=cdId Ou encore les matrices A + dId et (1/cd)B+(1/d)Id sont inverses l'unes de l'autres donc commutent. Cela devrait perme...
- 04 Mai 2012, 17:37
- Forum: ✯✎ Supérieur
- Sujet: matrice et application linéaire.
- Réponses: 4
- Vues: 604
(1)-(2) : Xo²-2XoXa+Xa²+Yo²-2YoYa+Ya²-(Xo²-2XoXb+Xb²+Yo²-2YoYb+Yb²)=0 -2XoXa+Xa²-2YoYa+Ya²+2XoXB-Xb²+2YoYb-Yb²=0 Je bloque... Il faudrait déjà que tu réduises cette expression ! tu obtiens unéquation du type K1x_0 + K2y_0=K3 (K1,K2,K3 constantes) D'où x_0 = K3/K1 - K2/K1y_0 Là tu remplace l'express...
- 24 Avr 2012, 09:34
- Forum: ✯✎ Supérieur
- Sujet: Centre d'un cercle
- Réponses: 4
- Vues: 706
Bonjour, Je suis amené à devoir déterminer le centre d'un cercle nommé O (j'aimerais avoir Xo et Yo en fonction des autres données) connaissant: - 2 points quelconques du cercle nommés A(Xa;Ya) et B(Xb;Yb) - le rayon du cercle R - le sens de rotation J'ai d'abord pensé à faire un système de 2 équat...
- 24 Avr 2012, 09:00
- Forum: ✯✎ Supérieur
- Sujet: Centre d'un cercle
- Réponses: 4
- Vues: 706
Le Skandalis est vraiment naze... Le Serge Lang est aussi indigeste... Le Queffelec, c'est vrai que c'est rédigé de façon assez brutale, mais pour l'avoir eu comme prof, je dirais que ça reste assez pédagogue. Donc bon, faut s'accrocher mais ça vaut le coup (Et il y a pas mal d'application sympas) ...
- 23 Avr 2012, 00:09
- Forum: ✯✎ Supérieur
- Sujet: bouquins de L3?
- Réponses: 30
- Vues: 1712
Désolé , je corrige : Est ce que la proposition suivante est correcte : $ \Big( \ x = 1 \ \mathrm{ou} \ y=2 \ \Big) \ \Longrightarrow \ x=1 $ Sinon, je ne comprends pas ton explication "judoboy". :cry: Merci pour votre aide. Pour que (A => B) soit vraie il faut que si tu supposes ...
- 18 Avr 2012, 18:31
- Forum: ✯✎ Supérieur
- Sujet: Logique
- Réponses: 7
- Vues: 631
Bonjour, Je voudrais savoir, si l'on considère un corps k par exemple, dans quels cas peut on écrire k(x)={ax+b | a,b dans k} (dans le meme genre que l'anneau de gauss où l'on a {a+ib |a,b dans Z } ? merci ey Si x \not \in k tu auras k(x)={ax+b | a,b dans k} à partir du moment où il existe un polyn...
- 18 Avr 2012, 18:25
- Forum: ✯✎ Supérieur
- Sujet: corps
- Réponses: 8
- Vues: 930
[quote="Cryptocatron-11"]J'ai du mal là aussi à voir le passage avec p(u)
J'ai essayé avec l'I.T mais j'arrive pas à retomber sur ton ||p(u)|| ² )
J'ai essayé avec l'I.T mais j'arrive pas à retomber sur ton ||p(u)|| ² )
- 12 Avr 2012, 19:16
- Forum: ✯✎ Supérieur
- Sujet: Inégalité de Cauchy-Swharz
- Réponses: 9
- Vues: 788
Il manque deux étapes entre les deux lignes (je suis assez surpris)
| u.w | ² <= || u || ²
et si tu note p(u) = |u.w|w, on peut réécrire la ligne précédente :
||p(u)|| ² <= || u - p(u)|| ² + ||p(u)||²
ce qui donne bien 0 <= ||u - |u.w|w||²
| u.w | ² <= || u || ²
et si tu note p(u) = |u.w|w, on peut réécrire la ligne précédente :
||p(u)|| ² <= || u - p(u)|| ² + ||p(u)||²
ce qui donne bien 0 <= ||u - |u.w|w||²
- 12 Avr 2012, 17:54
- Forum: ✯✎ Supérieur
- Sujet: Inégalité de Cauchy-Swharz
- Réponses: 9
- Vues: 788
Citation: Posté par Judoboy Je fais un bisou à celui qui me trouve une primitive de (x^3+3x)/((x²-1)^3). Je suis salement rouillé :/ Entièrement à la louche : La partie entière est nulle. On regarde la partie relative au pôle 1. On pose x=h+1 . On a \dfrac{x^3+3x}{(x+1)^3} = \dfrac{h^3+3h^2...
- 10 Avr 2012, 19:11
- Forum: ✯✎ Supérieur
- Sujet: Le fil des questions alakon
- Réponses: 64
- Vues: 3770
- 08 Avr 2012, 20:59
- Forum: ✯✎ Supérieur
- Sujet: intégrale impropre
- Réponses: 6
- Vues: 638
zork a écrit:je pense que ton équivalent est faux, on ne peut pas trouver d'équivalent lorsqu'il y a une exponentielle
Mais si l'équivalent
- 08 Avr 2012, 19:46
- Forum: ✯✎ Supérieur
- Sujet: intégrale impropre
- Réponses: 6
- Vues: 638
Réponse oui aux deux questions. Si on note v1, v2 la base de ker(f-id) proposée en correction, toi tu as simplement proposé v1, v1 + v2 qui en est également une base. Pour une base de ker(f - id) si on note w le vecteur proposé en correction, toi tu proposes -w qui est également une base de ker(f-id...
- 07 Avr 2012, 22:13
- Forum: ✯✎ Supérieur
- Sujet: calcul de base de ker f
- Réponses: 3
- Vues: 2380
Bah on a u et v deux vecteurs et par définition le produit scalaire de ces deux vecteurs c'est le nombre réél \vec{u}.\vec{v} définie par : \vec{u}\cdot\vec{v}=\frac12(||\vec{u}+\vec{v}||^2-||\vec{u}||^2-||\vec{v}||^2) Bah alors tu supposes que \vec u = x \vec i + y \vec j et \vec v = x'...
- 07 Avr 2012, 15:56
- Forum: ✯✎ Supérieur
- Sujet: Produit scalaire
- Réponses: 13
- Vues: 804
Si on se place dans un sev propre F de M^p pour une valeur propre \lambda \ne 0 , F est stable par M et le polynôme P = X^p-\lambda annule M . Mais puisque \lambda \ne 0 , le polynôme P a p racines distinctes. Un polynôme a racines simples annule M sur F, donc M est diagonalisable sur F. Puis M est ...
- 04 Avr 2012, 21:32
- Forum: ✯✎ Supérieur
- Sujet: exo intéressant
- Réponses: 3
- Vues: 569
Tu espères quoi ? Qu'on se mette à nos claviers et qu'on te rédige les solutions de tes exos ?
Le truc c'est que tu dises ce que tu as fait et sur quelle question tu bloques.
Le truc c'est que tu dises ce que tu as fait et sur quelle question tu bloques.
- 01 Avr 2012, 16:03
- Forum: ✯✎ Supérieur
- Sujet: espace vectorielle de dimension finie.....
- Réponses: 3
- Vues: 914
donc si K est borné, Il existe un M tel que quelque soit x appartenant à K, N(x)<= M Mais ce n'est pas le fait que les x soient bornés sur l'espace de départ qui compte ! C'est que les f (x) soit bornés sur l'espace d'arrivée. [HTML]si la fonction est continue donc dérivable donc admet un x tel que...
- 01 Avr 2012, 11:51
- Forum: ✯✎ Supérieur
- Sujet: boule fermée et ensemble compact
- Réponses: 9
- Vues: 1416
- 01 Avr 2012, 11:36
- Forum: ✯✎ Supérieur
- Sujet: boule fermée et ensemble compact
- Réponses: 9
- Vues: 1416
Pour le premier point, montre que 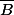 est fermé en considérant une suite convergente d'éléments de
est fermé en considérant une suite convergente d'éléments de 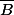 .
.
Pour le deuxième point,
Que peut-on dire de l'image d'un compact par une fonction continue ?
Que sait-on des compacts de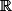 ?
?
Pour le deuxième point,
Que peut-on dire de l'image d'un compact par une fonction continue ?
Que sait-on des compacts de
- 01 Avr 2012, 10:46
- Forum: ✯✎ Supérieur
- Sujet: boule fermée et ensemble compact
- Réponses: 9
- Vues: 1416
Dinozzo13 a écrit:ha oui, effectivement : la convexité de.
C'est sûr que c'est trivial maintenant, mais comment le montrer ?
Tu dois connaître la propriété qu'une fonction est strictement convexe si sa dérivée est strictement croissante non ?
- 01 Avr 2012, 10:33
- Forum: ✯✎ Supérieur
- Sujet: Démontrer une inégalité
- Réponses: 6
- Vues: 729
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
