19 résultats trouvés
Revenir à la recherche avancée
orientation
bonjour, je viens d'avoir ma licence en maths générales et je sais pas trop ce que je vais faire exactement l'année prochaine . je veux faire un master maths appliquées mais j'hésite entre data science ou physique ou SITN (statistique informatique technique numérique ) ou maths fondamentales . en sa...
- 08 Juil 2017, 00:56
- Forum: ⚜ Salon Mathématique
- Sujet: orientation
- Réponses: 0
- Vues: 268
Re: integration 2
mdrrrrrrr 





- 18 Juin 2017, 21:45
- Forum: ✯✎ Supérieur
- Sujet: integration 2
- Réponses: 5
- Vues: 298
Re: integration 2
zygomatique a écrit:salut
et que vaut f_n hors de l'intervalle [-n, n ] ?
si elle y est nulle alors
mercii beaucoup


oui fn vaut 0 .
jlb a écrit:un ptit truc à corriger zygomatique!!
je vois pas, ou c'est ??
lambda au lieu de m ?
- 18 Juin 2017, 17:28
- Forum: ✯✎ Supérieur
- Sujet: integration 2
- Réponses: 5
- Vues: 298
integration 2
bonjour Voila un exo que je suis pas sure de l'avoir fais juste . on considere l'espace mesuré (\mathbb{R},\mathbb{B}( {\mathbb{R}),\lambda) ou \lambda est la mesure de Lebesgue . soit g definie de R dans R+ une fonction borélienne . on suppose qu'il existe une constante C telle que ...
- 18 Juin 2017, 14:01
- Forum: ✯✎ Supérieur
- Sujet: integration 2
- Réponses: 5
- Vues: 298
Re: integration
merciiii 

- 18 Juin 2017, 12:44
- Forum: ✯✎ Supérieur
- Sujet: integration
- Réponses: 8
- Vues: 779
Re: integration
je ne connais pas le théoreme des résidus . une autre question svp :P :P pour n>=1 ; x>0 I_n(x)=\int_0^{+\infty}\frac{dt}{(x^2+t^2)^n} \frac {1}{(t^2+x^2)^n} \sim \frac {1}{t^{2n} } je comprends pas pourquoi ça converge sur [0. infini[ pour moi ça converge pas sur ]0 ,1 ] mer...
- 17 Juin 2017, 23:26
- Forum: ✯✎ Supérieur
- Sujet: integration
- Réponses: 8
- Vues: 779
Re: integration
Salut ! Les problèmes se situent en 0 et en +\infty . Montre que la fonction u\mapsto \frac{1-\cos(u)}{u^2} est prolongeable par continuité en 0 . Pour +\infty , utilise le fait que 0\le 1-\cos(u) \le 2 et majore \int_1^A \frac{1-\cos(u)}{u^2} {\rm d} u par une intégrale I_A...
- 17 Juin 2017, 12:13
- Forum: ✯✎ Supérieur
- Sujet: integration
- Réponses: 8
- Vues: 779
integration
bonjour  :
:
je voudais savoir comment montrer que cette fonction est integrable (pour la mesure de Lebesgue sur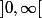
}{u^2}du)
je sais que l'equivalence en 0 c'est 1/2 mais ...
mercii


 :
:je voudais savoir comment montrer que cette fonction est integrable (pour la mesure de Lebesgue sur
je sais que l'equivalence en 0 c'est 1/2 mais ...
mercii
- 17 Juin 2017, 08:22
- Forum: ✯✎ Supérieur
- Sujet: integration
- Réponses: 8
- Vues: 779
Re: le sup d'une fonction
bonjour; j'aimerai savoir si je peux ecrire ceci : Sup_{0\leq x \leq 1} |f(x) - f(0)| \leq Sup_{0 \leq x\prec y\leq1} |f(x)- f(y) | et f est une fonction lipschitzienne sur [0,1] . si k est nombre de droite alors par définition de ce qu'il y a en indice du Sup c'est ...
- 30 Mai 2017, 19:13
- Forum: ✯✎ Supérieur
- Sujet: le sup d'une fonction
- Réponses: 10
- Vues: 904
Re: le sup d'une fonction
lionel52 a écrit:Hello! On note K la constante de Lips.
|f(x)| <= |f(0)| + |f(x)-f(0)| <= |f(0)| + K|x-0| <= |f(0)| + K
merciii de m'avoir répondu



- 30 Mai 2017, 18:53
- Forum: ✯✎ Supérieur
- Sujet: le sup d'une fonction
- Réponses: 10
- Vues: 904
Re: le sup d'une fonction
c'est bizarre, à droite on a un taux d'accroissement. et être k lipschitzienne, c'est quoi déjà la définition ? bonjour; definition d'une fonction K lipsch |f(x)-f(y)| \leq K |x-y| alors \frac{ |f(x)-f(y)|}{|x-y|}| \leq K OUI , c'est un taux d'accroissement , mais on...
- 30 Mai 2017, 17:27
- Forum: ✯✎ Supérieur
- Sujet: le sup d'une fonction
- Réponses: 10
- Vues: 904
Re: le sup d'une fonction
dans ton deuxième sup, tu as x et y et la réponse peut varier suivant les définitions de x et y si le sup porte sur y, la relation est sans doute vraie si le sup porte sur x, là elle est sans doute fausse merci de me répondre L est l'espace des fonctions lipschizienne de [0.1] ds R. je veux montrer...
- 29 Mai 2017, 23:42
- Forum: ✯✎ Supérieur
- Sujet: le sup d'une fonction
- Réponses: 10
- Vues: 904
Re: le sup d'une fonction
zygomatique a écrit:salut
pour répondre à ta question il suffit de savoir où se trouvent les quantificateurs implicites et leur nature ...
salut , je comprend pas ta réponse désolé .
- 29 Mai 2017, 16:53
- Forum: ✯✎ Supérieur
- Sujet: le sup d'une fonction
- Réponses: 10
- Vues: 904
le sup d'une fonction
bonjour;
j'aimerai savoir si je peux ecrire ceci :
 - f(0)| \leq Sup_{0 \leq x\prec y\leq1} |f(x)- f(y) |)
et f est une fonction lipschitzienne sur [0,1] .
merci de me répondre
j'aimerai savoir si je peux ecrire ceci :
et f est une fonction lipschitzienne sur [0,1] .
merci de me répondre
- 29 Mai 2017, 01:22
- Forum: ✯✎ Supérieur
- Sujet: le sup d'une fonction
- Réponses: 10
- Vues: 904
Re: l'ensemble des fonctions continues est complet
Il me semble qu'il y a un flou dans l'énoncé. Peux-tu dire que sont K, et E? De plus on définit la norme uniforme d'une fonction f à valeurs dans un corps R ou C, prise sur une partie X de R ou de C par sup_{x\in X} |f(x)| . Je ne comprends donc pas c'est quoi la définition de la norme unif...
- 26 Mai 2017, 18:42
- Forum: ✯✎ Supérieur
- Sujet: l'ensemble des fonctions continues est complet
- Réponses: 8
- Vues: 2530
Re: l'ensemble des fonctions continues est complet
salut soit Fn une suite de Cauchy de C([K,E] (muni de la norme uniforme) j'arrive pas a montrer que Fn est de Cauchy dans E (pour la norme E) ?? ça me semble contradictoire !! merci de m'avoir répondu je pense que ça veut dire que : a partir d'un certain rang les termes de la suite sont proche les ...
- 26 Mai 2017, 17:11
- Forum: ✯✎ Supérieur
- Sujet: l'ensemble des fonctions continues est complet
- Réponses: 8
- Vues: 2530
Re: l'ensemble des fonctions continues est complet
oui je sais le faire , en comparant la norme |.| et sup |.| ; mais vu qu'on ignore la norme de E alors aucune idée ; je sais pas si je pourrai prendre G une application continue sur E . Soit Gn une suite de E tq : Gn= G(Fn) et par definition de la contuinité de Gn on trouve que fn est de Cauchy sur E
- 26 Mai 2017, 01:09
- Forum: ✯✎ Supérieur
- Sujet: l'ensemble des fonctions continues est complet
- Réponses: 8
- Vues: 2530
Re: l'ensemble des fonctions continues est complet
aidez moi svp !!!!
:'( :'(
:'( :'(
- 26 Mai 2017, 00:05
- Forum: ✯✎ Supérieur
- Sujet: l'ensemble des fonctions continues est complet
- Réponses: 8
- Vues: 2530
l'ensemble des fonctions continues est complet
bonjour,
je dois démontrer que l'ensemble des fonctions continues sur un compact a valeurs dans un complet (muni de la norme uniforme) est complet
soit Fn une suite de Cauchy de C([K,E] muni de la norme uniforme
comment montrer que Fn est de Cauchy pour la norme de E?
merci de me répondre
je dois démontrer que l'ensemble des fonctions continues sur un compact a valeurs dans un complet (muni de la norme uniforme) est complet
soit Fn une suite de Cauchy de C([K,E] muni de la norme uniforme
comment montrer que Fn est de Cauchy pour la norme de E?
merci de me répondre

- 25 Mai 2017, 22:26
- Forum: ✯✎ Supérieur
- Sujet: l'ensemble des fonctions continues est complet
- Réponses: 8
- Vues: 2530
- 19 résultats trouvés - Page 1 sur 1
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
