23 résultats trouvés
Revenir à la recherche avancée
Partition et ensemble des parties
Bonjour, Dans un livre il est affirmé que si E est un ensemble fini, l'ensemble des éléments de P(E) (ensemble des parties de E) est une partition de P(E). Par exemple si A={1,2,3) P(A) contient {1} et {1,2} or leur intersection n'est pas vide puisque c'est 1, donc l'ensemble des éléments de P(E) n'...
- 21 Mar 2018, 19:32
- Forum: ⚜ Salon Mathématique
- Sujet: Partition et ensemble des parties
- Réponses: 3
- Vues: 613
anneau commutatif infère
Bonjour,
On dit que Z/mZ est un anneau commutatif infère avec m différent de 1.
Mais qu'en est-il pour m=0?
Z/0Z= { ... , {-1} , {0} , {1} , {2}, ...}
Quel serait l'inverse de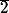 par exemple dans cet anneau?
par exemple dans cet anneau?
Merci
On dit que Z/mZ est un anneau commutatif infère avec m différent de 1.
Mais qu'en est-il pour m=0?
Z/0Z= { ... , {-1} , {0} , {1} , {2}, ...}
Quel serait l'inverse de
Merci
- 15 Fév 2018, 08:26
- Forum: ⚜ Salon Mathématique
- Sujet: anneau commutatif infère
- Réponses: 5
- Vues: 651
Fonctions réciproques
Bonjour,
J'aurais une question a propos de la symétrie des fonctions réciproques.
Je sais qu'elles sont symétriques par rapport à l'axe y=x mais comment le démontre t-on? Merci
J'aurais une question a propos de la symétrie des fonctions réciproques.
Je sais qu'elles sont symétriques par rapport à l'axe y=x mais comment le démontre t-on? Merci
- 13 Nov 2017, 22:14
- Forum: ⚜ Salon Mathématique
- Sujet: Fonctions réciproques
- Réponses: 3
- Vues: 273
à propos du théorème de la valeur intermédiaire
Bonjour,
Voici mon problème:
Dans un livre il est écrit que le théorème de la valeur intermédiaire nous dit que tout nombre réel compris entre deux éléments de f(I) est aussi dans f(I).
Ma question est: en quoi le théorème de la valeur intermédiaire nous dit ce qui est écrit précedemment?
Merci
Voici mon problème:
Dans un livre il est écrit que le théorème de la valeur intermédiaire nous dit que tout nombre réel compris entre deux éléments de f(I) est aussi dans f(I).
Ma question est: en quoi le théorème de la valeur intermédiaire nous dit ce qui est écrit précedemment?
Merci
- 31 Oct 2017, 19:39
- Forum: ⚜ Salon Mathématique
- Sujet: à propos du théorème de la valeur intermédiaire
- Réponses: 8
- Vues: 620
Re: inégalité à prouver
C'est de la logique simple: (néanmoins je simplifie un peu les détails) Soit P: x^2\geq (2-e)/(2+e) , Q : (1-x^2)/(1+x^2)<-1+e et R: x^2>(2-e)/e Il faut montrer que P implique Q. Mais on a vu que Q est équivalent à R. Il faut donc montrer que P implique R. Ma...
- 23 Oct 2017, 19:59
- Forum: ⚜ Salon Mathématique
- Sujet: inégalité à prouver
- Réponses: 10
- Vues: 624
Re: inégalité à prouver
Je comprends bien pourquoi P implique R si (2-e)/e<(2-e)/(2+e). Mais si (2-e)/e>=(2-e)/(2+e) cela ne devient plus évident mais c'est là où je suis perdu c'est que démontrer P implique R reste "jouable", peut-être par des détours compliqués mais "pas impossible" . Vous n'êtes pas ...
- 22 Oct 2017, 18:11
- Forum: ⚜ Salon Mathématique
- Sujet: inégalité à prouver
- Réponses: 10
- Vues: 624
Re: inégalité à prouver
On se demande juste si avec l'hypothèse x^{2}\geq \frac{2-\varepsilon }{2+\varepsilon } est-ce que cela donne x^{2}> \frac{2-\varepsilon }{\varepsilon } mais je ne comprends pas quel est votre raisonnement derrière le fait de dire que \frac{2-\varepsilon }{2+\varepsilon }>\frac{2-\varepsilon }{\vare...
- 22 Oct 2017, 14:36
- Forum: ⚜ Salon Mathématique
- Sujet: inégalité à prouver
- Réponses: 10
- Vues: 624
Re: inégalité à prouver
Ben moi je trouve 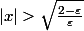
- 22 Oct 2017, 09:33
- Forum: ⚜ Salon Mathématique
- Sujet: inégalité à prouver
- Réponses: 10
- Vues: 624
Re: inégalité à prouver
Merci. En partant de l'inégalité à prouver on se rend compte que c'est l'inégalité posée comme condition initiale qui est fausse.
- 21 Oct 2017, 22:51
- Forum: ⚜ Salon Mathématique
- Sujet: inégalité à prouver
- Réponses: 10
- Vues: 624
inégalité à prouver
Bonjour, je n'arrive pas à démontrer l'inégalité qui suit:
Soit tel que
tel que 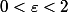 ; si
; si 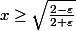 alors
alors 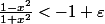
Merci de votre aide.
Soit
Merci de votre aide.
- 21 Oct 2017, 22:21
- Forum: ⚜ Salon Mathématique
- Sujet: inégalité à prouver
- Réponses: 10
- Vues: 624
nombres complexes
Bonjour,
Je ne comprends pas comment on passe d'une expression à l'autre:
}}{e^{i\alpha }-ie^{i\left(\beta -\frac{\pi }{2} \right)}})
Cordialement,
Moki45
Je ne comprends pas comment on passe d'une expression à l'autre:
Cordialement,
Moki45
- 21 Sep 2017, 21:13
- Forum: ⚜ Salon Mathématique
- Sujet: nombres complexes
- Réponses: 1
- Vues: 285
Re: exercice forme exponentielle 2
Euréka! Je sais pourquoi il y a un facteur négatif devant le cos. Parce que dans la forme exponentielle le facteur devant le e doit être positif.
- 21 Sep 2017, 10:14
- Forum: ⚜ Salon Mathématique
- Sujet: exercice forme exponentielle 2
- Réponses: 1
- Vues: 324
exercice forme exponentielle 2
Bonsoir, à tous Dans un exercice il est demandé de trouver la forme exponentielle de e^{i\alpha}+e^{i\beta } La réponse est la suivante: e^{i\alpha}+e^{i\beta }= \begin{cases} & 2\cos \left(\frac{\alpha -\beta }{2}\right)e^{i\frac{\alpha +\beta }{2}} \text{ quand } 2\cos \left(\frac{...
- 20 Sep 2017, 21:01
- Forum: ⚜ Salon Mathématique
- Sujet: exercice forme exponentielle 2
- Réponses: 1
- Vues: 324
exercice forme exponentielle
Bonjour à tous, Pour transformer un nombre complexe sous la forme exponentielle on doit factoriser par le module. Mais dans ce cas comment s'y prendre sachant que si on factorise par le module on est bloqué pour trouver l'argument qui ne découle pas de manière évidente. Voici le nombre complexe à tr...
- 30 Aoû 2017, 22:17
- Forum: ⚜ Salon Mathématique
- Sujet: exercice forme exponentielle
- Réponses: 1
- Vues: 318
Re: colinéarité vecteurs complexes
Je vois mieux maintenant. Merci bien Pseuda
- 24 Aoû 2017, 08:42
- Forum: ⚜ Salon Mathématique
- Sujet: colinéarité vecteurs complexes
- Réponses: 2
- Vues: 1490
colinéarité vecteurs complexes
Bonjour, Dans un exercice il est dit que pour que deux vecteurs soient colinéaires il faut et il suffit que le rapport des deux nombres complexes est un réel. Il est ensuite dit que cela revient à écrire u(v barre)-v(u barre)=0. Comment montre t-on que u(v barre)-v(u barre)=0 équivaut à dire que les...
- 23 Aoû 2017, 21:31
- Forum: ⚜ Salon Mathématique
- Sujet: colinéarité vecteurs complexes
- Réponses: 2
- Vues: 1490
Faire des maths tout seul
Bonjour, Avez vous des conseils pour faire des maths de manière autodidacte? Je fais des maths par curiosité, j'aimerais comprendre le fonctionnement des maths. Mais je suis bloqué parfois, je ne comprends pas les démonstrations. Quel conseils donner pour quelqu'un qui voudrais faire des maths mais ...
- 04 Juin 2017, 10:37
- Forum: ⚜ Salon Mathématique
- Sujet: Faire des maths tout seul
- Réponses: 0
- Vues: 516
Re: Questions variées ouvertes
Bonjour,
Votre réponse est claire zygomatique , mais une classe d'équivalence je ne vois pas trop ce que c'est. L'ensemble des parties de l'ensemble singleton {2} ça m'est un peu compliqué. Merci pour l'effort de clarté quand bien même.
Votre réponse est claire zygomatique , mais une classe d'équivalence je ne vois pas trop ce que c'est. L'ensemble des parties de l'ensemble singleton {2} ça m'est un peu compliqué. Merci pour l'effort de clarté quand bien même.
- 04 Juin 2017, 09:53
- Forum: ⚜ Salon Mathématique
- Sujet: Questions variées ouvertes
- Réponses: 13
- Vues: 957
Re: Questions variées ouvertes
Je viens de me rendre compte que la racine complexe n'est pas la même chose que racine d'un nombre réel positif. 1 à bien deux racines complexes: 1 et -1 car leur carré donne 1 et que la racine complexe (carrée) de x est de définition: racinecpx(x) est le nombre z tel que z²=x. Par contre dans le me...
- 25 Mai 2017, 10:15
- Forum: ⚜ Salon Mathématique
- Sujet: Questions variées ouvertes
- Réponses: 13
- Vues: 957
Re: Questions variées ouvertes
Mais sinon, où est l'erreur dans le paradoxe suivant: la règle est i²=-1------------------------------>par définition ou bien la racinecpx(-1(ou i²))=i ou -i -->par définition à partir de là: racinecpx(-49)=racinecpx(i²*49) =7i ou bien -7i alors on peut aussi écrire: 1=racinecpx(-1*(-1)) racinecpx(-...
- 25 Mai 2017, 10:01
- Forum: ⚜ Salon Mathématique
- Sujet: Questions variées ouvertes
- Réponses: 13
- Vues: 957
- 23 résultats trouvés - Page 1 sur 2 • 1, 2
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
