9 résultats trouvés
Revenir à la recherche avancée
Re: Calcul différentiel : Théorème de la submersion
Comment écrire  en fonction de
en fonction de 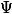 ?
?
- 24 Avr 2017, 12:51
- Forum: ✯✎ Supérieur
- Sujet: Calcul différentiel : Théorème de la submersion
- Réponses: 19
- Vues: 1477
Re: Calcul différentiel : Théorème de la submersion
Bon j'ai f(x)+y=(z_1,z_2) \in E\times F_2 Donc d\Psi(a,0)=\begin{pmatrix} \frac{\partial z_1}{\partial x} & \frac{\partial z_1}{\partial y} \\ \frac{\partial z_2}{\partial x} & \frac{\partial z_2}{\partial y}\end{pmatrix} Question 4 : montrer que c'est inversible.. Ba...
- 24 Avr 2017, 08:54
- Forum: ✯✎ Supérieur
- Sujet: Calcul différentiel : Théorème de la submersion
- Réponses: 19
- Vues: 1477
Re: Calcul différentiel : Théorème de la submersion
Oui! Bien joué !
- 23 Avr 2017, 12:32
- Forum: ✯✎ Supérieur
- Sujet: Calcul différentiel : Théorème de la submersion
- Réponses: 19
- Vues: 1477
Re: Calcul différentiel : Théorème de la submersion
C'est ce que je pensais aussi qu'il fallait trouver une matrice 2*2 et pour le déterminant c'est facile apres, mais je ne sais pas comment faire pour trouver une telle matrice alors qu'on arrive pas dans un produit cartésien a l'arrivée.. Ou alors je sais pas comment faire pour diviser en 2 l'espace...
- 22 Avr 2017, 20:18
- Forum: ✯✎ Supérieur
- Sujet: Calcul différentiel : Théorème de la submersion
- Réponses: 19
- Vues: 1477
Re: Calcul différentiel : Théorème de la submersion
Oui exacte ! Je suis passé à la deuxième partie du DM (je suppose qu'on est dans la même classe...) : le théorème de l'immersion ! À la question 3, il faut écrire d\Psi(a,0) sous la forme d'une matrice par blocs avec \Psi :\Omega\times F_2 \to F=F_1\oplus F_2, (x,y)\mapsto f(x...
- 22 Avr 2017, 16:08
- Forum: ✯✎ Supérieur
- Sujet: Calcul différentiel : Théorème de la submersion
- Réponses: 19
- Vues: 1477
Re: Calcul différentiel : Théorème de la submersion
La jacobienne de \Phi(a)=\left(\frac{\partial a_1}{\partial a_1} \quad \frac{\partial a_1}{\partial a_2} \quad \quad \quad \frac{\partial f(a)}{\partial a_1} \quad \frac{\partial f(a)}{\partial a_2} \right)
- 20 Avr 2017, 17:36
- Forum: ✯✎ Supérieur
- Sujet: Calcul différentiel : Théorème de la submersion
- Réponses: 19
- Vues: 1477
Re: Calcul différentiel : Théorème de la submersion
Merci je n'avais pas pensé à la projection !
En revanche, rien ne nous dit que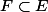
Pour ce qui est du signe "identifiable" c'est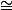 , mais ce n'est peut-être pas le signe identifiable..
, mais ce n'est peut-être pas le signe identifiable..
En revanche, rien ne nous dit que
Pour ce qui est du signe "identifiable" c'est
- 20 Avr 2017, 17:26
- Forum: ✯✎ Supérieur
- Sujet: Calcul différentiel : Théorème de la submersion
- Réponses: 19
- Vues: 1477
Re: Calcul différentiel : Théorème de la submersion
Pour cette question tu fais la jacobienne de 
- 20 Avr 2017, 17:09
- Forum: ✯✎ Supérieur
- Sujet: Calcul différentiel : Théorème de la submersion
- Réponses: 19
- Vues: 1477
Re: Calcul différentiel : Théorème de la submersion
Bonjour, Je dois avoir le même sujet que Pick et je voudrais savoir ce que veut dire ce que sont des ensembles identifiables et comment prouver qu'ils le sont ? Ayant \Phi : E=E_1\bigoplus E_2\to E_1\times F=:\~E, x\mapsto (x_1,f(x_1,x_2)) sachant que E_1=ker(df(a)) e...
- 20 Avr 2017, 16:55
- Forum: ✯✎ Supérieur
- Sujet: Calcul différentiel : Théorème de la submersion
- Réponses: 19
- Vues: 1477
- 9 résultats trouvés - Page 1 sur 1
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
