68 résultats trouvés
Revenir à la recherche avancée
Re: Structures algébriques
Salut. C'est uniquement un problème de définition (donc sans grand intérêt) : la tendance majoritaire à l'heure actuelle est plutôt de considérer que la terme "anneau" désigne un anneau unitaire (et d'utiliser le terme de "pseudo anneau" dans le cas non unitaire). Par contre, je...
- 10 Sep 2025, 14:30
- Forum: ✯✎ Supérieur
- Sujet: Structures algébriques
- Réponses: 3
- Vues: 2094
Structures algébriques
Bonjour , Voici l 'exercice: Soit A , un anneau booléen. On suppose que A est intègre. Démontrer que A est isomorphe à {0} ou à Z/2Z. Quelqu'un peut me confirmer qu'un anneau intègre ne peut pas être isomorphe à {0} car il a au moins 2 éléments et donc que la question de cet exercice est un peu tord...
- 10 Sep 2025, 08:22
- Forum: ✯✎ Supérieur
- Sujet: Structures algébriques
- Réponses: 3
- Vues: 2094
Re: Structures algébriques
C'est OK je viens de trouver c'est juste la première égalité(*) qui n'est pas correct
Merci
Merci
- 07 Sep 2025, 18:53
- Forum: ✯✎ Supérieur
- Sujet: Structures algébriques
- Réponses: 4
- Vues: 2268
Structures algébriques
Bonsoir tout le monde , On veut montrer que G est abélien à partir de l'hypothèse suivante : Soit (G,.) un groupe et f : G--->G tel que f(x)=x^3, un endomorphisme surjectif de G. voici la première partie de solution de l exercice que je ne comprends pas car elle me semble pas correct : 1)Soit y appa...
- 07 Sep 2025, 18:42
- Forum: ✯✎ Supérieur
- Sujet: Structures algébriques
- Réponses: 4
- Vues: 2268
Re: Structures algébriques
Je viens de trouver merci Pour ceux que ca intéresse : Soit t appartient à Phi(x), il existe donc f appartenant à H tel f(x)=t. Or y appartient à Phi(x),il existe donc g appartenant à H tel que g(x)=y. on en déduit que x=f^-1(t)=g^-1(y) donc t=(f o g^-1)(y) appartient à Phi(y). Conclusion Phi(x) c P...
- 12 Juil 2025, 15:37
- Forum: ✯✎ Supérieur
- Sujet: Structures algébriques
- Réponses: 1
- Vues: 3018
Structures algébriques
Bonjour, Voici l'exercice : Soit (G, . ) un groupe . a)Montrer que l 'ensemble des automorphismes de G, muni de la loi o, est un groupe , noté Aut(G). b)Soit H un sous-groupe de Aut(G) et Phi: G--->P(G) qui à x associe {f(x) , f appartenant à H}; (Phi est appelé l' orbite de x sous H ).Vérifier que ...
- 12 Juil 2025, 15:14
- Forum: ✯✎ Supérieur
- Sujet: Structures algébriques
- Réponses: 1
- Vues: 3018
Re: arithméttique
Je pense avoir trouvé (à moins du contraire): soient x, y appartenant à N* tels que x+y=n+1. si x=y : on a pgcd(x,y)=x=f(x,y) si y>x : y=x+(y-x)=n+1-x<=n donc pgcd(x,y)=pgcd(x,y-x)=f(x,y-x)=f(x,(y-x)+x)=f(x,y) Et on démontre de même le cas x>y l' hérédité est démontrée Et la réciproque est triviale ...
- 07 Avr 2025, 10:04
- Forum: ✯✎ Supérieur
- Sujet: arithméttique
- Réponses: 1
- Vues: 2445
arithméttique
Bonjour, L'exercice : Trouver toutes les applications f:N*xN* --> N* telles que : pour tout a et b appartenant à N* : f(a,a)=a f(a,b)=f(b,a) f(a,b)=f(a,a+b) La solution ; Montrer : pour tout n de N* ( quelque soit (x,y) appartenant à N*xN*,( x+y=n =>pgcd(x,y)=f(x,y) )) par récurrence forte. ma solut...
- 06 Avr 2025, 16:23
- Forum: ✯✎ Supérieur
- Sujet: arithméttique
- Réponses: 1
- Vues: 2445
Re: Nombres premier , coefficient binomial
Salut, Si on prend par exemple p=4 (non premier) et k=2, (qui divise p) alors k divise {p\choose k}\!=\!6 . Donc il n'y a pas de contradiction à ton hypothèse. Il y a éventuellement plus simple, mais on peut commencer par montrer que, pour tout nombre premier p, la valuation p-adique de {n\choose k...
- 23 Mar 2025, 20:22
- Forum: ✯✎ Supérieur
- Sujet: Nombres premier , coefficient binomial
- Réponses: 4
- Vues: 2675
Re: Nombres premier , coefficient binomial
Bonjour, Qu'as-tu essayé ? Bonjour, j'ai essayé ce qui suit : Si p n 'est pas premier il existe k , 1<k<p tel que k divise p et donc k divise \binom{p}{k} et mon but serait d'aboutir à une contradiction comme montrer p!/[(p-k)!k!k] n'est pas un entier mais je ne vois pas pour le moment comment .
- 23 Mar 2025, 10:55
- Forum: ✯✎ Supérieur
- Sujet: Nombres premier , coefficient binomial
- Réponses: 4
- Vues: 2675
Nombres premier , coefficient binomial
Bonjour,
Soit p un entier naturel , et quelque soit l'entier k, 1<k<p , p divise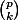 ,
,
montrer que p est premier.
Si quelqu'un peut m'aider pour cette démonstration
Merci
Soit p un entier naturel , et quelque soit l'entier k, 1<k<p , p divise
montrer que p est premier.
Si quelqu'un peut m'aider pour cette démonstration
Merci
- 22 Mar 2025, 23:34
- Forum: ✯✎ Supérieur
- Sujet: Nombres premier , coefficient binomial
- Réponses: 4
- Vues: 2675
Re: Somme
Super merci !
- 11 Mar 2025, 15:28
- Forum: ✯✎ Supérieur
- Sujet: Somme
- Réponses: 3
- Vues: 1997
Somme
Bonjour,
Comment arrive t-on à ce résultat ?
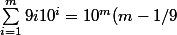+ 1/9)
Merci
Comment arrive t-on à ce résultat ?
Merci
- 10 Mar 2025, 22:40
- Forum: ✯✎ Supérieur
- Sujet: Somme
- Réponses: 3
- Vues: 1997
Re: arithmétique
Désolé je me suis trompé l énoncé c'est 2x + 3y +5z= 1.
Donc tout rentre dans l 'ordre et merci pour ton aide
Donc tout rentre dans l 'ordre et merci pour ton aide
- 27 Fév 2025, 14:17
- Forum: ✯✎ Supérieur
- Sujet: arithmétique
- Réponses: 4
- Vues: 1414
Re: arithmétique
Donc 2(x+z)=-3(y+z) et donc -3(y+z) est pair donc y + z est pair non ?
- 27 Fév 2025, 14:05
- Forum: ✯✎ Supérieur
- Sujet: arithmétique
- Réponses: 4
- Vues: 1414
arithmétique
Bonjour,
Résoudre dans Z ^3 : 2x + 3y +5z=0.
La solution débute par :
Soit (x,y,z) convenant alors Alors y + z est impair d' ou 2 cas etc.
Je ne comprends pas pourquoi y + z est impair
merci
Résoudre dans Z ^3 : 2x + 3y +5z=0.
La solution débute par :
Soit (x,y,z) convenant alors Alors y + z est impair d' ou 2 cas etc.
Je ne comprends pas pourquoi y + z est impair
merci
- 27 Fév 2025, 13:35
- Forum: ✯✎ Supérieur
- Sujet: arithmétique
- Réponses: 4
- Vues: 1414
Re: Application
Bonjour ,
Merci pour ton retour .
Ta démonstration est correct mais tu utilises des variables (x, y , z ) pour la démonstration ,
ce que je souhaite justement éviter .
Merci pour ton retour .
Ta démonstration est correct mais tu utilises des variables (x, y , z ) pour la démonstration ,
ce que je souhaite justement éviter .
- 18 Aoû 2024, 10:04
- Forum: ✯✎ Supérieur
- Sujet: Application
- Réponses: 2
- Vues: 420
Application
Bonsoir, Soit une application f : E---> F On suppose que quelque soit A appartenant à P(E) f^{-1}(f(A))=A . Comment fait t on pour démontrer que pour tout ensemble A et B de P(E) f(A)n f(B) c f(AnB) mais uniquement en substituant les ensembles par leur définition de départ (si c'est ...
- 16 Aoû 2024, 19:42
- Forum: ✯✎ Supérieur
- Sujet: Application
- Réponses: 2
- Vues: 420
Re: Dénombrement
GaBuZoMeu a écrit:Bonjour,
Oui.
Merci .
- 02 Juin 2024, 20:08
- Forum: ✯✎ Supérieur
- Sujet: Dénombrement
- Réponses: 2
- Vues: 494
- 02 Juin 2024, 14:43
- Forum: ✯✎ Supérieur
- Sujet: Dénombrement
- Réponses: 2
- Vues: 494
- 68 résultats trouvés - Page 1 sur 4 • 1, 2, 3, 4
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

