Forum de Mathématiques: Maths-Forum

Non, c'est pas difficile. . C'est l'exemple idéal.

D'accord merci

Bonsoir ben341.... Que.....?

D'accord merci énormément pour vos éclaircissements..... À bientôt (au prochain problème)

Bonsoir.. Je vois mieux maintenant en fait H_{a} est surjective si il existe un x\in E / pour tout g\in C(f) , H_{a}(g)=x donc g(a)=x et comme x\in E g(a)=\lambda_{0}a +..........+\lambda_{n-1}f^{n-1}(a) car (a,...........,f^{n-1}(a)) est une b...

Je t'avoue que je ne voisvraiment pas comment..... s'écrit donc comment ? ()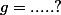
Il suffit de prendre pour quel ?

donc pour tout x de E car est une base de .

D'accord merci... Et comment à partir de ceci je peux affirmer que 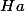est surjective.

J'essaie.... f^{n-1}(a)\neq0 donc quelque soit a\in E [\tex] , [tex] a n'appartient pas à kerf^{n-1} car f^{n-1}(a) \neq0 .soit \lambda_{0}......\lambda_{n-1}\in R^{n} . Supposons que \lambda_{0}a+\lambda_{1}f(a)+......+\lambda_{n-1}f^{n-1}(a) =\vec{0} . Composons cet...

Salut.. Pour ton exo s'il n'était pas question d'utiliser les fonctions usuelles tu pouvais utiliser le théorème de l'inégalité des accroisements finis 1ère formulation. Et tu pourra faire ceci même pour ta 2ème fonction f(x)=3x-3 sur l'interval donné . f(x)=\frac{2x^2+1}{x^2+3} pour...

Lol lol lol Merci pour la leçon... Comment je peux m'y prendre pour la surjection et l'injection.

D'accord... Mais j'ai vraiment besoin d'une petite explication ; Pourquoi Ha est un isomorphisme du fait que la famille { a,......... f(n-1)(à) } est une base de E .

D'accord... Ce ne serait pas la troisième question parce qu'il est demandé de montrer à question là que C(f) est le sous espace vectoriel engendré par la famille ( ide, f, ............ , f^(n-1) ) et là je comptais montrer que c'est une famille libre.

Et est-ce suffisant de montrer que l'image de l'élément neutre de l'ensemble de départ par l'application est l'élément neutre de l'ensemble d'arrv pour affirmer que c'est un morphisme

D'accord.... Pour la question suivante je pense faire ceci Pour montrer que (H)a est un isomorphisme je vais montrer que c'est un morphisme en premier temps et ensuite montrer qu'elle est injective et surjective i.e bijective. La caractéristique d'un morphisme est que l'image de l'élément neutre de ...

*Soit g € C(f) et lmd €R on a :
f•lmdg = f(lmdg) = lmd f(g) car f est une app linéaire et de plus f(g)=g(f) car g appartient à C(f) , f•lmdg = lmdg(f)= lmdg•f. Donc lmdg € C(f).
*soit g1 et g2 apprtnt à C(f) on a :
(g1+g2)•f=g1•f + g2•f = f•g1 + f•g2 = f•(g1 + g2) d'où g1 + g2 apprtnt à C(f).

D'accord je me lance

Je suis partagé entre la première et ceci
pour tout x € E, t•f(x) - f•t(x)= t(f(x)) - f(t(x)) or f est un endo nilpotent i.e f est d'indice de nilpotence 1 ssi f est l'endo nulle i.e f(x)=t(x) pour tout x de E. On a alors t•f(x) - f•t(x) = 0 pour tout x de E . t•f(x) = f•t(x) d'où t € C(f)

D'accord merci... C'est correct ?

1. *Je montre que l'application nulle € C(f)
Soit t: E---->E
x------>0E l'application nulle
on a g•t(x) - t•g(x)= g(t(x)) - t(g(x))= 0 i.e g•t(x) = t•g(x) donc t € C(f).
C'est juste la première étape( pour montrer que C(f) est non vide).