Forum de Mathématiques: Maths-Forum

Je ne comprend pas pourquoi le fait que l'un des sommets aient n+1 degrés et l'autre 0 degrés ça vérifié la propriété?

EDIT : En fait, il y a même bien plus simple en faisant une récurrence de 2 en 2 : si tu part d'un graphe ayant la propriété demandée, que tu rajoute un premier sommet que tu relie à tout les autres puis que tu rajoute un second sommet que tu laisse isolé, ça te donne de nouveau un graphe ayant la ...

Bonjour, j'ai cette exercice a faire que j'ai commencé mais j'ai du mal a continuer On souhaite montrer la propriété Pn suivante, pour tout entier \geq 2: Il existe un graphe à n sommets tel que, pour tout i \in [0,n-2] un des n sommets a degré i - en particulier , exactement deux sommets ont même d...

Je dois aussi montrer que tout graphe sans triangle a n sommet possede (au moins) un sommet de degré inférieur ou égal a \frac{n}{2} . Je me suis dit que je pouvait commencer en supposant le contraire mais je ne sais pas comment continuer. Supposons tout graphe sans triangle a n sommets possede (auc...

Bonjour, j'ai un exercice sur les graphe sans triangle. Un graphe sans triangle est un graphe qui ne contient pas de cycle de longueur 3. On veut montrer la propriété suivante: P(n): Pour tout graphe sans triangle à n sommets et m arêtes m \leq \frac{n^2}{4} Je dois montrer que cette preuve n'en ai ...

La continuité uniforme? Mais on ne sais pas si f est uniforme.

Oui pardon c'est n qui tend vers l'infinie je rectifie mon erreur.

Bonjour, j'ai f:[a,b] --->R une fonction continue. Pour tout entier naturel n>0: I_{n}=\sum_{k=0}^{n-1} \int_{a_{k}}^{a_{k+1}} f(t) \, \mathrm{d}t avec a_{k}=a+k \frac{b-a}{n} Et je dois montrer que \lim\limits_{n \to \infty}$I_{n}=\int_{a}^{b} f(t) \, \mathrm{d}t Ca me fait penser a...

Donc l'ensemble des vecteur isotropes c'est (0,0). Je pose {uE | q(u)=0}={x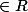 | (x,x)=0 et (x,-x)=0}={x 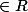| x=0}
Je sais pas si je peut le formuler comme ca

Comme on a x^2-y^2=0 on a x^2=y^2 donc x=y ou x=-y donc u=(x,x) ou u=(x,-x)

Donc on a q(u)=0 <=> x=0 et y=0 donc on aurait u=(0,0) avec u=(x,y) ?

J'ai une derniere question je dois determiner l'ensemble des ses vecteurs isotropes mais je ne sais pas trop comment faire. En tout cas commencer.

Moi j'ai pas l'impression qu'on puisse faire une reducion de Gauss vu que les deux termes sont carré.

BOnjour j'aimerai bien savoir comment faire pour trouver la signature d'une forme quadratique par exemple q((x,y))=

Code: Tout sélectionner

x^2-y^2

est-ce que c'est direct ou il faut faire une reduction de gauss?

Je vois pas trop, mais A c'est un sous espace quelconque de E, apres une forme linéaire sur E qui est nul?

Finalement j'ai bien reussi a montrer que f+g \in P^{\perp} je ne sais pas pourquoi je me suis embrouillé comme ca. Par contre j'ai une autre question mais je ne sias pas du tout par quoi commencé pour montrer ca 2.Montrer que pour toute forme linéaire \psi sur A se prolonge en une forme linéaire \P...

Je pense que ca veut dire f

Donc j'ai juste a dire que pour tout f,g on a f+g donc est stable par addition et multiplication par un scalaire donc est bien un s-e-v de E*. C'est suffisant? Je trouve que ca ne prouve pas forcement que f+g

D'accord je comprend ce que tu veut dire .
Mais si est une partie de E* comment je vais faire pour montrer que c'est linéaire avec les combinaison linéaire f et g

Oui mais c'est quoi par exemple tq f,g. C'est ca qui m'empeche un peu d'avancer parceque je sais que je dois montrer que f+kg