Forum de Mathématiques: Maths-Forum

Très bien, merci de m'avoir aidée !

Bonne soirée

Je vous remercie vraiment de m'avoir aidé !

J'ai bien compris le problème maintenant.

Bonne soirée à vous

Alors a = 1 ou a = -1

f'(a) = 10a - 6 = 0 avec a =0,6

Est-ce cela ?

Après avoir repéré une erreur et modifié mon développement, voici mon expression finale :


Est-ce le taux d'accroissement ? Je pensais pouvoir réduire encore cette expression

Bonsoir Lalo, a tu ne le connais pas ! Tu sais que la tangente en x = ? passe par (0,0) donc que x=0 et y =0 Tu sais simplement que ton équation de la tangente en un x à découvrir (le fameux a !) s'écrit y = f'(a)(x-a)+f(a) avec le x=0 et le y=0 et ça donne . . . ? ===> soit 0 = f'(a)(0 - a) + f(a)...

Salut, Je comprend vraiment pas ce que tu fout avec ton a=0. Ce que tu calcule, c'est la tangente à la courbe au point d'abscisse a . On te demande si cette tangente passe ou pas par le point (0,0). Tu peut m'expliquer quel raisonnement (foireux) t'incite à penser que ce qu'il y a d'écrit juste au ...

Je pense que mon erreur vient du développement de l'expression :


=
= ...

J'ai utilisé la formule du taux d'accroissement avec les valeurs :

f(-2) =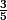

f(-2 + h) =

mais mon résultat final ne me semble pas juste

J'ai calculé f'(a) :

f'(a) = 10a - 6 donc si a = 0, f'(a) = -6

C'est le nombre

Il rentre en compte dans les nombres et fonctions dérivés mais je ne sais pas comment t'expliquer davantage à quoi il correspond.

C'est-à-dire ?

Voici ce que j'ai déjà essayé :

T : y = f'(a)(x-a)+f(a)
avec a = 0 donc f(a) = 5 et f'(a) = -6

alors T : y = -6x + 5 ce qui ne peut pas être juste.

Bonjour,

Je n'arrive pas à résoudre ce problème, pourriez-vous m'aider ?

Trouver les points de la courbe C de la fonction f(x) = 5x² - 6x + 5 pour lesquels la tangente passe par l'origine.

Merci

Bonjour,

J'ai un problème pour résoudre cet exercice, pourriez-vous m'aider ?

Déterminer le taux d'accroissement de la fonction f définie sur R par f(x) = .
En déduire le nombre dérivé de f en -2.

Merci