Forum de Mathématiques: Maths-Forum

Bpnjour, en notant H le produit des racines en développant P= c(X-x1)...(X-xp) le terme constant est obtenu en ne prenant jamais X mais que des xk il vaut donc (-1)^p C H donc produit des racines = (-1)^p terme constant / coefficient de X^P oK, merci encore Fahr541 :we: sinon effectivement sue ! (ra...

G'day , ah bah quoi dire merci :we: c'est toujours formidable de trouver des gens toujours présents pour aider et partager :++: pour cette question j'ai essayé justement de develloper avec p=3 pour voir ce qui se passe , mais j'ai pas pu généraliser , c'est donc le cas général , pour un poly. de deg...

ben en admettant celà , je te souhaite une bonne nuit :we:

merci bieen !

ok donc coefficient dominant c'est le coefficient du facteur du plus haut degré dans mon expresion soit

c ça ?

OK , je vais réctifier , sinon...

je suis perdue là ... :triste:

pourquoi ce coefficient dominant ? peux-tu détailler stp ?

ah ben merci bien :we:

donc on peut écire comme factorisation :

c bon ?

oui c'est la suite .. la question qui précède celle là était juste de vérifier que : sin(na)= sin^n(a) (\sum_{k=0}^{[\frac{(n-1)}{2}]} (-1)^k C_{2k+1}^{n} cotan^{n-2k-1} c facile avec ce qui a été montré précédemment . sinon on a pas mentionné ce polynome de tchyb...

bonsoir,

enfin connecté fahr541 , peux-tu regarder stp ?

salut fahr541 , j'ai encore besoin de ton aide pour la suite de cet exo si possible . on pose : P(x)= \sum_{k=0}^{k=p} (-1)^k C_{2p+1}^{2k+1} x^{p-k} 1) je dois montrer que : P(x_k)=0 tel que x_k = cot^2(\frac{k\pi}{2p+1}) puis en déduire une factorisation à P(x) . 2)...

trés bien détaillé :++:
j'ai bien compris , je n'aurais plus ce souci grâce à vous :we:


merci bien !
G'day

bonjour

merci mais j'ai encore besoin de vos lumières :we:
- y manque pas une combinaison qq part ?
- pouvez-vous m'expliquer pourquoi la partie entière de (n-1)/2 ?

merci
G'day

je ne crois pas que ça marche comme ça !

celà dépend si n= 4k+3 ou n=4k+1 puisque et

bonsoir, on me demande de calculer sin(na) en fonction de sina et cosa je trouve : sin(na) = C_n^1 (cosa)^{n-1} sina - C_n^3 (cosa)^{n-3} (sina)^3 +....(+/- ??) mais je sais pas quoi mettre à la fin , ça dépend de la parité de n n'est-ce pas ? j'aimerais aussi...

je remonte , je cherche toujours ce vieux exo :lol:

pour la parité de ,il faut encore faire une reccurence ?
:hein:

ok c bon , merci Blueberry :we:


j'essaierai le reste et je te tiens au courant ou cas ou je bloque :mur:

salut ! je n'arriive même pas à commencer cet exo :triste: soient : u_n = (2+\sqrt{3})^n + (2-\sqrt{3})^n et v_n = sin\left(\frac{\pi}{2}(2+\sqrt{3})^n) 1) montrer que pour tout n de IN , il existe \alpha_n , \beta_n , a_n et b_n tel que : (2+\sqrt{3})^n= \alp...

je remonte , je cherche toujours cet exo lol :we:

bonsoir ,

donc pour tt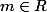 f admet une unique solution , puisque l'image de l'ensemble de départ par f c'est R .
mais celà m'étonne car la question n'a aucun sens dans ce cas !