26 résultats trouvés
Revenir à la recherche avancée
Re: DM Première S
Résultat trouvé, grâce a géogébra et beaucoup de travaille de nuit.
- 29 Oct 2016, 00:01
- Forum: ✎✎ Lycée
- Sujet: DM Première S
- Réponses: 9
- Vues: 2609
Re: DM Première S
C'est important, pourriez vous m'aidez ?????!!!!
- 28 Oct 2016, 23:36
- Forum: ✎✎ Lycée
- Sujet: DM Première S
- Réponses: 9
- Vues: 2609
Re: DM Première S
Je bloque pour la question 3, pouvez vous m'aidez je ne sais pas comment faire du tous.
- 28 Oct 2016, 22:49
- Forum: ✎✎ Lycée
- Sujet: DM Première S
- Réponses: 9
- Vues: 2609
Re: DM Première S
merci de vos réponses
- 28 Oct 2016, 16:17
- Forum: ✎✎ Lycée
- Sujet: DM Première S
- Réponses: 9
- Vues: 2609
Re: DM Première S
J'ai un peux avancé: x^2+\pi \times \left(\frac{10-x}{2} \right)^2 x^2+\pi \times \frac{\left(10-x \right)^2}{4} x^2+\pi \times \frac{100-10x-10x+x^2}{4} x^2+\pi \times \frac{x^2-20x+100}{4} x^2+\pi \times\left(\frac{x^2}{4}-5x+25 \right) x^2+\frac{x^2}{4}\pi +\pi(-5)...
- 28 Oct 2016, 15:28
- Forum: ✎✎ Lycée
- Sujet: DM Première S
- Réponses: 9
- Vues: 2609
Re: DM Première S
merci, un oublie en recopiant.
J'ai corrigé, normalement la suite est cohérente. Mais ça ne m'avance pas plus que ça, car maintenant j'ai plus la forme ax²+bx+c
J'ai corrigé, normalement la suite est cohérente. Mais ça ne m'avance pas plus que ça, car maintenant j'ai plus la forme ax²+bx+c
- 28 Oct 2016, 14:30
- Forum: ✎✎ Lycée
- Sujet: DM Première S
- Réponses: 9
- Vues: 2609
DM Première S
Bonjours, voici l’intitulé du sujet: Sur un segment AB de longueur 10, on place un point M mobile. On construit un carré de coté [AM] et un disque de diamètre [MB] . 1) Faire une figure. (faite ci-dessous). 2) Sachant que AM = x , démonter que la somme des aires du carré et du disque est minimum lor...
- 28 Oct 2016, 14:01
- Forum: ✎✎ Lycée
- Sujet: DM Première S
- Réponses: 9
- Vues: 2609
Re: Aire maximale d'un rectangle inscrit dans un triangle éq
Merci beaucoup pour votre aide
- 27 Oct 2016, 15:48
- Forum: ✎✎ Lycée
- Sujet: Aire maximale d'un rectangle inscrit dans un triangle équila
- Réponses: 18
- Vues: 1626
- 27 Oct 2016, 15:47
- Forum: ✎✎ Lycée
- Sujet: Aire maximale d'un rectangle inscrit dans un triangle équila
- Réponses: 18
- Vues: 1626
Re: Aire maximale d'un rectangle inscrit dans un triangle éq
Donc la réponse est qu'il faut placer le point P à 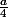 en partant de B.
en partant de B.
Le point Q à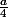 en partant de C.
en partant de C.
Le point M doit être ou ?
Le point N doit être ou ?
Le point Q à
Le point M doit être ou ?
Le point N doit être ou ?
- 27 Oct 2016, 15:40
- Forum: ✎✎ Lycée
- Sujet: Aire maximale d'un rectangle inscrit dans un triangle équila
- Réponses: 18
- Vues: 1626
Re: Aire maximale d'un rectangle inscrit dans un triangle éq
merci.
Mais je bloque sur le a/2 que j'ai trouvé en faisant X2, qu'est ce que c'est ?
Mais je bloque sur le a/2 que j'ai trouvé en faisant X2, qu'est ce que c'est ?
- 27 Oct 2016, 15:31
- Forum: ✎✎ Lycée
- Sujet: Aire maximale d'un rectangle inscrit dans un triangle équila
- Réponses: 18
- Vues: 1626
Re: Aire maximale d'un rectangle inscrit dans un triangle éq
Donc le maximum est 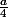
Mais du cous je fais quoi de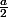 ?
?
Mais du cous je fais quoi de
- 27 Oct 2016, 15:21
- Forum: ✎✎ Lycée
- Sujet: Aire maximale d'un rectangle inscrit dans un triangle équila
- Réponses: 18
- Vues: 1626
Re: Aire maximale d'un rectangle inscrit dans un triangle éq
Pour X1 je sais pas si c'est bon mais on pourais faire: X1 = \frac{-a\sqrt{3}+a\sqrt{3}}{-4\sqrt{3}} X1 = \frac{0}{-4\sqrt{3}} X1 = 0 Pour X2 : X2 = \frac{-a\sqrt{3}-a\sqrt{3}}{-4\sqrt{3}} X2 = \frac{2(-a\sqrt{3})}{-4\sqrt{3}} X2 = \frac{2a\sqrt{3}}{4\sqrt{3}} X2 = \frac{a\sqrt{3}}{2\sqrt{3}...
- 27 Oct 2016, 15:14
- Forum: ✎✎ Lycée
- Sujet: Aire maximale d'un rectangle inscrit dans un triangle équila
- Réponses: 18
- Vues: 1626
Re: Aire maximale d'un rectangle inscrit dans un triangle éq
J'ai essayer de calculer, mais je bloque à X1 et X2 Aire PMNQ = \left[PQ \right]\times \left[PM \right] Aire PMNQ = (a-2x)\times (x\sqrt{3}) Aire PMNQ = -2\sqrt{3}x^2+a\sqrt{3}x a=-2\sqrt{3} b=a\sqrt{3} c=0 \delta =b^2-4ac = (a\sqrt{3})^2-4\times (-2\sqrt{3})\times 0 ...
- 27 Oct 2016, 15:11
- Forum: ✎✎ Lycée
- Sujet: Aire maximale d'un rectangle inscrit dans un triangle équila
- Réponses: 18
- Vues: 1626
Re: Aire maximale d'un rectangle inscrit dans un triangle éq
ok, je vais faire ça. Merci beaucoup
- 27 Oct 2016, 14:43
- Forum: ✎✎ Lycée
- Sujet: Aire maximale d'un rectangle inscrit dans un triangle équila
- Réponses: 18
- Vues: 1626
Re: Aire maximale d'un rectangle inscrit dans un triangle éq
Oui j'ai essayé mais je ne trouvais pas comment faire. Et quand tu simplifie c'est parce-que tu fais: \left[PM \right] = \frac{a\sqrt{\frac{3}{4}}\times x}{\frac{1}{2}a} \left[PM \right] = \frac{\frac{\sqrt{3}}{2}\times x}{\frac{1}{2}} \left[PM \right] = x\sqrt{3} !? Merci beaucoup. Et du cous pour ...
- 27 Oct 2016, 14:35
- Forum: ✎✎ Lycée
- Sujet: Aire maximale d'un rectangle inscrit dans un triangle équila
- Réponses: 18
- Vues: 1626
Aire maximale d'un rectangle inscrit dans un triangle équila
bonjours, J'ai un DM a faire, mais je bloque sur un calcule. Intitulé si dessous. [BA] = [AC] = [CB] = a [BP] = [QC] = x [PQ] = [MN] = a-2x J'ai fait la hauteur du triangle, que je nomme h. Et je crée un point G au milieu de [BC]. Le segment [AG] est le segment h. Pour calculer la longueur du segmen...
- 27 Oct 2016, 14:02
- Forum: ✎✎ Lycée
- Sujet: Aire maximale d'un rectangle inscrit dans un triangle équila
- Réponses: 18
- Vues: 1626
Re: Aire d'une partie de cercle
ok, c'est finis, merci alors
- 27 Oct 2016, 09:25
- Forum: ✎✎ Lycée
- Sujet: Aire d'une partie de cercle
- Réponses: 12
- Vues: 6944
Re: Aire d'une partie de cercle
En refaisant je trouve \pi \left(\frac{16-(x^2-8x+16)}{4}+\frac{-x^2}{4} \right) \pi \left(\frac{16-x^2+8x-16}{4}+\frac{-x^2}{4 \right)} \pi \left(\frac{-x^2+8x}{4}+\frac{-x^2}{4} \right) \pi \left(\frac{2\left(-x^2 \right)+8x}{4} \right) \pi \left(...
- 26 Oct 2016, 22:26
- Forum: ✎✎ Lycée
- Sujet: Aire d'une partie de cercle
- Réponses: 12
- Vues: 6944
Re: Aire d'une partie de cercle
mais si je mais 2x ca change rien a mon probleme l'erreur est toujours la car je trouverais ) et non
et non )
- 26 Oct 2016, 22:15
- Forum: ✎✎ Lycée
- Sujet: Aire d'une partie de cercle
- Réponses: 12
- Vues: 6944
- 26 résultats trouvés - Page 1 sur 2 • 1, 2
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
