24 résultats trouvés
Revenir à la recherche avancée
Re: Vitesse et temps de déplacement dans R2
Ah bon? Pourtant j'essaie d'abord de chercher n pour lequel T sera minimum non... M est mon point, m son abscisses, n ma distance MB et v oui la vitesse sur l'axe des abscisses et on définie T en fonction de v non? Ce que tu veux dire c'est que je dois prendre v comme si c'était une vitesse fixée? M...
- 02 Nov 2016, 09:49
- Forum: ✯✎ Supérieur
- Sujet: Vitesse et temps de déplacement dans R2
- Réponses: 11
- Vues: 899
Re: Vitesse et temps de déplacement dans R2
Bonsoir à vous deux :) En m'y repentant voilà ce que j'ai réussi à faire : On pose M (m;0) (comme on me l'avait conseillé) un point de l'axe des abscisses avec m compris entre 0 et 3. On a alors, grâce au théorème de Pythagore appliqué au triangle AOM: AM ^{2} = A0^{2} + OM^{2} AM^{2}= 1^{2} + OM^{2...
- 30 Oct 2016, 18:20
- Forum: ✯✎ Supérieur
- Sujet: Vitesse et temps de déplacement dans R2
- Réponses: 11
- Vues: 899
Re: Vitesse et temps de déplacement dans R2
Ahhhh oui je vois mieux d'accord, je vais m'y repencher, j'ai compris le principe !
Merci beaucoup, je reviendrais vers toi au besoin
Bonne soirée !
Merci beaucoup, je reviendrais vers toi au besoin
Bonne soirée !
- 28 Oct 2016, 17:43
- Forum: ✯✎ Supérieur
- Sujet: Vitesse et temps de déplacement dans R2
- Réponses: 11
- Vues: 899
Re: Récurrence
Petite erreur de ma part... Puisque je dérive en fonction de t, le t disparait dans le dernier membre de ma dérivée après mes équations équivalentes.
Ainsi que le t après le -at dans ma dernière résolution...
Petite étourderie
Ainsi que le t après le -at dans ma dernière résolution...
Petite étourderie
- 28 Oct 2016, 12:34
- Forum: ✯✎ Supérieur
- Sujet: Récurrence
- Réponses: 2
- Vues: 201
Re: Vitesse et temps de déplacement dans R2
Bonjour,
Tout d'abord, merci pour ta réponse. Pourquoi changes-tu mon énoncé?
Il s'agit bien de B = (3,0) dans l'exercice...
Je ne comprend pas bien ce que l'on essaye de faire en posant le point M = (m,0) peux-tu m'expliquer plus en détails?
Merci d'avance !
Tout d'abord, merci pour ta réponse. Pourquoi changes-tu mon énoncé?
Il s'agit bien de B = (3,0) dans l'exercice...
Je ne comprend pas bien ce que l'on essaye de faire en posant le point M = (m,0) peux-tu m'expliquer plus en détails?
Merci d'avance !
- 28 Oct 2016, 12:25
- Forum: ✯✎ Supérieur
- Sujet: Vitesse et temps de déplacement dans R2
- Réponses: 11
- Vues: 899
Récurrence
Bonjour, Cet exercice me donne vraiment du fil à retordre... Je sais tout à fait faire des récurrences mais celle-ci... Exercice: Montrer par récurrence sur k qu'il existe un polynôme de degré k, qui sera noté P _{k} (t), tel que P _{k} e ^{-t} soit une primitive de t ^{k} e ^{-t} . (On dérivera t ^...
- 28 Oct 2016, 12:21
- Forum: ✯✎ Supérieur
- Sujet: Récurrence
- Réponses: 2
- Vues: 201
Vitesse et temps de déplacement dans R2
Bonjour, Voici un de mes exercices. J'ai plutôt compris le principe mais je me demande si mes réponses sont bien celles attendues... Voudriez vous bien me dire si je suis partie dans la bonne direction? Exercice: Dans le plan R ^{2} , quel temps minimum T(v) faut-il pour se rendre du point de coordo...
- 28 Oct 2016, 11:02
- Forum: ✯✎ Supérieur
- Sujet: Vitesse et temps de déplacement dans R2
- Réponses: 11
- Vues: 899
Re: inégalité
Pareil j'ai bien compris ! Très bon pédagogue !
- 17 Oct 2016, 11:09
- Forum: ✯✎ Supérieur
- Sujet: inégalité
- Réponses: 10
- Vues: 502
Re: inégalité
17 pour les deux ... Donc  ?
?
- 16 Oct 2016, 19:33
- Forum: ✯✎ Supérieur
- Sujet: inégalité
- Réponses: 10
- Vues: 502
Re: Suite adjacentes
Oui pardon j'avais oublié de précisé que l'on m'avait aidé...
- 16 Oct 2016, 18:59
- Forum: ✯✎ Supérieur
- Sujet: Suite adjacentes
- Réponses: 2
- Vues: 340
Re: démonstration
Ah oui d'accord merci je vois comment passer de l'une à l'autre !
Merci beaucoup d'avoir pris le temps de m'aider et de bien m'expliquer sur plusieurs topic
Merci beaucoup d'avoir pris le temps de m'aider et de bien m'expliquer sur plusieurs topic
- 16 Oct 2016, 18:55
- Forum: ✯✎ Supérieur
- Sujet: démonstration
- Réponses: 8
- Vues: 322
Re: inégalité
Oui désolée je ne trouve pas les crochets sur le mac... A la fin j'arrive à: \mid y^{2013} - x^{2013}\mid \leq 2013\mid y - x \mid Mais normalement je devrais avoir: \mid y^{2013} - x^{2013}\mid \leq 2013\mid x - y \mid Est-ce normale et l'affirmation est fausse ou je me suis trompée?.. Je peux vous...
- 16 Oct 2016, 18:51
- Forum: ✯✎ Supérieur
- Sujet: inégalité
- Réponses: 10
- Vues: 502
Merci beaucoup :D
Oh oui milles excuses erreur de distraction je le sais en plus c'est logique... Ensuite j'ai donc fait : -> 2 \sqrt{n+1} > \sqrt{n+1} + \sqrt{n} => \sqrt{n+1} > \sqrt{n} Ce qui est vrai puisque n > 0 -> 2 \sqrt{n} < \sqrt{n+1} + \sqrt{n} => \sqrt{n}<\sqrt{n+1} Ce qui est aussi vrai car n > 0 On a do...
- 16 Oct 2016, 18:01
- Forum: ✯✎ Supérieur
- Sujet: Inégalité
- Réponses: 9
- Vues: 306
Suite adjacentes
Coucou tout le monde, voici un nouvel exercice qui me donne du fil à retorde ! Soit une fonction f : {0,1} -> {0,1} 1. Montrer que si f est continue, alors elle admet (au moins) un point fixe, ce qui signifie qu'il existe (au moins un) \alpha tel que f(\alpha) = \alpha ( Indice : utiliser le TVI) 2....
- 16 Oct 2016, 14:50
- Forum: ✯✎ Supérieur
- Sujet: Suite adjacentes
- Réponses: 2
- Vues: 340
Re: Inégalité
Donc c'est équivalent à :
2
Mais je ne vois pas ou on veut en venir...
2
Mais je ne vois pas ou on veut en venir...
- 16 Oct 2016, 14:09
- Forum: ✯✎ Supérieur
- Sujet: Inégalité
- Réponses: 9
- Vues: 306
Re: démonstration
Ah merci oui je m'étais trompée au début ...
Du coup l'affirmation est fausse? car on a lnb / lna au lieu de lna / lnb
Du coup l'affirmation est fausse? car on a lnb / lna au lieu de lna / lnb
- 16 Oct 2016, 14:01
- Forum: ✯✎ Supérieur
- Sujet: démonstration
- Réponses: 8
- Vues: 322
Re: démonstration
f'(x) = ( 1/x ) / ln(x) = ln(x) / x
en effet je m'étais trompée...
En recommençant je suis maintenant bloquée ici:
}{c}))
en effet je m'étais trompée...
En recommençant je suis maintenant bloquée ici:
- 16 Oct 2016, 13:02
- Forum: ✯✎ Supérieur
- Sujet: démonstration
- Réponses: 8
- Vues: 322
Re: Inégalité
Je l'ai fait et j'obtient : 
Mais après?
Mais après?
- 16 Oct 2016, 12:51
- Forum: ✯✎ Supérieur
- Sujet: Inégalité
- Réponses: 9
- Vues: 306
Re: démonstration
Grace à ton aide j'arrive à:
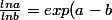 * \frac{exp(c)}{lnc})
Mais je ne sais plus comment continuer pour retomber sur la réponse attendue...
Mais je ne sais plus comment continuer pour retomber sur la réponse attendue...
- 16 Oct 2016, 12:43
- Forum: ✯✎ Supérieur
- Sujet: démonstration
- Réponses: 8
- Vues: 322
Re: Inégalité
Il faut que je fasse la forme conjugué de celui du milieu? Car je ne comprend pas comment faire même avec la forme conjuguée que je maitrise bien pour les limites par exemple...
- 16 Oct 2016, 12:29
- Forum: ✯✎ Supérieur
- Sujet: Inégalité
- Réponses: 9
- Vues: 306
- 24 résultats trouvés - Page 1 sur 2 • 1, 2
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
