30 résultats trouvés
Revenir à la recherche avancée
Re: Montrer q'une matrice est inversible sans déterminant
Merci Ben, je me doutais qu'il y avait un problème avec ma première idée.
- 07 Nov 2018, 21:17
- Forum: ✯✎ Supérieur
- Sujet: Montrer q'une matrice est inversible sans déterminant
- Réponses: 4
- Vues: 1071
Montrer q'une matrice est inversible sans déterminant
Bonjour, Je voudrais savoir comment montrer que la matrice A=\begin{pmatrix}a & b \\ c & d\end{pmatrix} est inversible ssi ad-bc est non nul, mais sans passer par la notion de déterminant. Je pensais dire qu'elle n'est pas inversible ssi a=c et b=d ie ad-bc=0 mais ca me parais trop facile, i...
- 07 Nov 2018, 20:26
- Forum: ✯✎ Supérieur
- Sujet: Montrer q'une matrice est inversible sans déterminant
- Réponses: 4
- Vues: 1071
Dérivée de vecteur
Bonjour, Alors voilà, dans un DM de SII (MPSI) on est amené à dériver un vecteur position pour obtenir le vecteur vitesse du point G_{3} dans la base 3 (il y a 3 bases dans l'exo: 0, 2 et 3). Voilà, la dérivée du vecteur: \vec{V_{3/0}(G_{3})}=\frac{d\vec{OG_{3}}}{dt}_{/B_{0}}=\frac{d(f&#...
- 16 Sep 2018, 14:04
- Forum: ✯✎ Supérieur
- Sujet: Dérivée de vecteur
- Réponses: 0
- Vues: 301
Re: Démonstration de l'inégalité arithmetico-geometrique
Merci pour vos retours ! Après, il nous est demandé de démontrer l'inégalité arithmético-géométrique, à savoir : \forall n \in N^{*}, \forall (x_{1}, x_{2}, .., x_{n}) \in R_{+}^{n}, \sqrt[n]{x_{1}x_{2}...x_{n}} \leq \frac{x_{1}+x_{2}+..+x_{n}}{n} En utilisant ce que l'on a montré précédemme...
- 09 Sep 2018, 09:49
- Forum: ✯✎ Supérieur
- Sujet: Démonstration de l'inégalité arithmetico-geometrique
- Réponses: 8
- Vues: 3713
Re: Démonstration de l'inégalité arithmetico-geometrique
Merci de votre réponse.
J'étais arrivé jusque là, mais c'est le passage de f(x1+...+xn)+f(x(n+1)+...+x2n) à f(x1) + ... + f(x2n) où je bloque. Ne connaissant pas la fonction, je ne sait pas comment la decomposer, ou montrer que la second partie est supérieure à la première
J'étais arrivé jusque là, mais c'est le passage de f(x1+...+xn)+f(x(n+1)+...+x2n) à f(x1) + ... + f(x2n) où je bloque. Ne connaissant pas la fonction, je ne sait pas comment la decomposer, ou montrer que la second partie est supérieure à la première
- 08 Sep 2018, 13:54
- Forum: ✯✎ Supérieur
- Sujet: Démonstration de l'inégalité arithmetico-geometrique
- Réponses: 8
- Vues: 3713
Démonstration de l'inégalité arithmetico-geometrique
Bonjour, Je suis en MPSI, on a pas encore commencé le programme de maths et on a cet exo a faire : Soit f:R \rightarrow R vérifiant pour tout (x,y) \in R^{2} : f(\frac{x+y}{2}) \leq \frac{f(x)+f(y)}{2} . On veut prouver : \forall n \in N, \forall (x_{1}, ... , x_{...
- 08 Sep 2018, 10:39
- Forum: ✯✎ Supérieur
- Sujet: Démonstration de l'inégalité arithmetico-geometrique
- Réponses: 8
- Vues: 3713
Problème 1 du concours général de 2016
Bonjour, M'étant inscrit au concours général de maths 2018, je commence d'ores et déjà à m'entraîner sur les sujets des années précédentes. En ce moment je traie le sujet de 2016 et je bloque à cette question: "Montrer que, pour tout x\ge5 , on a (2x+1)^3\le2(2x-1)^3 ." Pou...
- 04 Déc 2017, 15:38
- Forum: ✎✎ Lycée
- Sujet: Problème 1 du concours général de 2016
- Réponses: 5
- Vues: 493
Re: Démontrer que 333^777 - 777^333 est divisible par 37
Ah oui ! Pourquoi je l'avais pas vu !? 
Merci !
Merci !
- 11 Sep 2017, 16:16
- Forum: ✎✎ Lycée
- Sujet: Démontrer que 333^777 - 777^333 est divisible par 37
- Réponses: 2
- Vues: 1423
Démontrer que 333^777 - 777^333 est divisible par 37
Bonjour, En spé maths, je doit démontrer que N = 333^777 - 777^333 est divisible par 37. Dans des question précédente, j'ai déjà démontré que tout nombre du type AAA, AAAAAA ou ABABAB est divisible par 37: - AAA: 111*A = 37*3A - AAAAAA: 111 111*A = 37*3003A - ABABAB: 37(2730A+273B) Mais là je bloque...
- 11 Sep 2017, 15:40
- Forum: ✎✎ Lycée
- Sujet: Démontrer que 333^777 - 777^333 est divisible par 37
- Réponses: 2
- Vues: 1423
Re: probabilités astronomiques (1°S)
D'accord, merci
C'est tordu tout de même de mettre ça en contrôle ! Sans tableur ni logiciels !!
Merci à tous
C'est tordu tout de même de mettre ça en contrôle ! Sans tableur ni logiciels !!
Merci à tous
- 23 Mar 2017, 10:09
- Forum: ✎✎ Lycée
- Sujet: probabilités astronomiques (1°S)
- Réponses: 12
- Vues: 536
Re: probabilités astronomiques (1°S)
C'est la loi binomiale !? Je ne l'ai pas encore faite. Mais je trouve: 5 parmi 20 = 15504
- 22 Mar 2017, 17:09
- Forum: ✎✎ Lycée
- Sujet: probabilités astronomiques (1°S)
- Réponses: 12
- Vues: 536
Re: probabilités astronomiques (1°S)
Donc dans 21, il y a :
21 = 1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1
Soit:
21 = 1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1
21 =2+2+2+4+5+3+3
Donc c'est "5 parmi 20"
Mais je ne comprend pas comment vous obtenez 56 pour votre exemple
Merci de m’éclaircir ce point.
21 = 1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1
Soit:
21 = 1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1
21 =2+2+2+4+5+3+3
Donc c'est "5 parmi 20"
Mais je ne comprend pas comment vous obtenez 56 pour votre exemple
Merci de m’éclaircir ce point.
- 22 Mar 2017, 16:17
- Forum: ✎✎ Lycée
- Sujet: probabilités astronomiques (1°S)
- Réponses: 12
- Vues: 536
Re: probabilités astronomiques (1°S)
Je viens de trouver un super site qui a résolu mon problème : http://www.dcode.fr/solveur-cryptarithme ! Il suffit de rentrer A+B+C+D+E+F=21 et ca trouve 720 solutions. En plus en regardant, les valeurs des lettres vont de 1 à 6 automatiquement ! Merci dcode.fr Donc p(X=-2) = p(21) = 720/46 656 = 5/...
- 22 Mar 2017, 15:50
- Forum: ✎✎ Lycée
- Sujet: probabilités astronomiques (1°S)
- Réponses: 12
- Vues: 536
Re: probabilités astronomiques (1°S)
Je ne pense pas être capable de faire ce type de programme, c'est pas encore dans mes cordes 
Pourriez-vous mettre l’algorithme correspondant s'il vous plait ?
Pourriez-vous mettre l’algorithme correspondant s'il vous plait ?
- 22 Mar 2017, 14:46
- Forum: ✎✎ Lycée
- Sujet: probabilités astronomiques (1°S)
- Réponses: 12
- Vues: 536
probabilités astronomiques (1°S)
Bonjour, Il y a un mois j'ai eu un contrôle de 2h sur les proba (entre autres) et mon prof vient de le transformer en dm. Je bloque sur une question. Voici l'énoncé: "On lance 3 fois de suite 2 dés non pipés: un dé rouge et un dé vert ; on note ainsi chaque lancer comme un couple de valeurs (v;...
- 22 Mar 2017, 14:31
- Forum: ✎✎ Lycée
- Sujet: probabilités astronomiques (1°S)
- Réponses: 12
- Vues: 536
Re: Équation (y-x)(y+x) = a
Merci du coup de main, c'était tellement évident que j'étais passé à côté 
Le couple (16;20) est solution du système.
Merci pour l'aide que vous m'avez apporté

Le couple (16;20) est solution du système.
Merci pour l'aide que vous m'avez apporté
- 25 Oct 2016, 13:08
- Forum: ✎✎ Lycée
- Sujet: Équation (y-x)(y+x) = a
- Réponses: 26
- Vues: 1846
Re: Équation (y-x)(y+x) = a
oui, j'ai dut me tromper en passant de y² - x² = 12² à y - x = 12
Il faut faire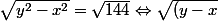(y+x)} = 12 \Leftrightarrow \sqrt{y-x} \times \sqrt{y+x} = 12)
Il faut faire
- 25 Oct 2016, 11:52
- Forum: ✎✎ Lycée
- Sujet: Équation (y-x)(y+x) = a
- Réponses: 26
- Vues: 1846
Re: Équation (y-x)(y+x) = a
d'où vient 10*24 ?
- 25 Oct 2016, 11:42
- Forum: ✎✎ Lycée
- Sujet: Équation (y-x)(y+x) = a
- Réponses: 26
- Vues: 1846
Re: Équation (y-x)(y+x) = a
x = 12 et y = 24
- 25 Oct 2016, 11:17
- Forum: ✎✎ Lycée
- Sujet: Équation (y-x)(y+x) = a
- Réponses: 26
- Vues: 1846
Re: Équation (y-x)(y+x) = a
Voici l'énoncé: Un potager est formé de 2 carrés. Il a fallu 144 m de bois pour entourer les deux carrés et l'on a semé de la pelouse sur les 144 m² de surface qui séparent les 2 carrés. Calculer les côtés de chaque carré. Voici le schéma indiqué à côté de l'énoncé : schéma énoncé.png J'ai nomé x le...
- 25 Oct 2016, 10:39
- Forum: ✎✎ Lycée
- Sujet: Équation (y-x)(y+x) = a
- Réponses: 26
- Vues: 1846
- 30 résultats trouvés - Page 1 sur 2 • 1, 2
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
