18 résultats trouvés
Revenir à la recherche avancée
Bonjour,
je suis bloqué sur un exercice:
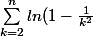= ln(\prod_{k=2}^{n}{1-\frac{1}{k^2}}) =ln(\prod_{k=2}^{n}{1}-\prod_{k=4}^{n+2}{\frac{1}{k}}))
je ne sais pas si j'ai bon pour l'instant
Merci d'avance
- par achoum
- 10 Sep 2016, 15:05
-
- Forum: ✎✎ Lycée
- Sujet: somme de logarithme
- Réponses: 3
- Vues: 490
je pensé qu' il fallait faire ca mais suis d'accord que ca ne sert a rien
- par achoum
- 04 Sep 2016, 11:13
-
- Forum: ✎✎ Lycée
- Sujet: Logarithme neperien
- Réponses: 35
- Vues: 1042
Comment avez vous trouvé la borne gauche de cet intervalle solution ? Comment avez vous trouvé la borne droite de cet intervalle solution ? J'ai besoin de calculs détaillés (de voir la démarche logique que vous avez suivi afin de comprendre si vous avez compris ou pas) 2ln(x)<1 exp(2ln(x))<exp(1) x...
- par achoum
- 04 Sep 2016, 11:07
-
- Forum: ✎✎ Lycée
- Sujet: Logarithme neperien
- Réponses: 35
- Vues: 1042
Non pour définir la borne gauche de l'intervalle, il faut se poser la poser la question de savoir pour quelles valeurs de x l'expression ln(x) existe ? La fonction ln(x) est définie pour x>0 (par définition) Question intermédiaire : ------------------------------- Pour quelles valeurs de x la fonct...
- par achoum
- 04 Sep 2016, 10:40
-
- Forum: ✎✎ Lycée
- Sujet: Logarithme neperien
- Réponses: 35
- Vues: 1042
Ok si tout ceci à été assimilé alors on passe à l'étape suivante : Résoudre : 2ln(x)<1 Avec tous les calculs détaillés bien sûr (que ce soit pour déterminer la borne gauche et la borne droite de l'intervalle solution) ;) 2ln(x)<1 ln(x)<1/2 exp(ln(x)<exp(1/2) x<exp(1/2) x=]1;exp(1/2)[ 1 car ...
- par achoum
- 04 Sep 2016, 10:29
-
- Forum: ✎✎ Lycée
- Sujet: Logarithme neperien
- Réponses: 35
- Vues: 1042
Ok si tout ceci à été assimilé alors on passe à l'étape suivante : Résoudre : 2ln(x)<1 Avec tous les calculs détaillés bien sûr (que ce soit pour déterminer la borne gauche et la borne droite de l'intervalle solution) ;) 2ln(x)<1 ln(x)<1/2 exp(ln(x)<exp(1/2) x<exp(1/2) x=]1;exp(1/2)[ 1 car ...
- par achoum
- 04 Sep 2016, 10:20
-
- Forum: ✎✎ Lycée
- Sujet: Logarithme neperien
- Réponses: 35
- Vues: 1042
anthony_unac a écrit:Exact et comment as tu trouvé la borne gauche de cet intervalle ?
en trouvant les solutions de ln(x-1)
qui me donne x-1>0
=x>1
- par achoum
- 04 Sep 2016, 10:06
-
- Forum: ✎✎ Lycée
- Sujet: Logarithme neperien
- Réponses: 35
- Vues: 1042
anthony_unac a écrit:Donc
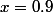
convient puisqu'il appartient à l'intervalle

Donc je suppose que j'ai faux
il appartient al'intervalle x=]1;1+e[
- par achoum
- 04 Sep 2016, 09:59
-
- Forum: ✎✎ Lycée
- Sujet: Logarithme neperien
- Réponses: 35
- Vues: 1042
anthony_unac a écrit:C'est exactement ça !
)
n'a de sens que si

est positif (et c'était la mise en garde de Lostounet)
Pourriez vous à présent me donner la solution (complète) de
<1)
Donc la réponse c'est : x =]0;e+1[
- par achoum
- 04 Sep 2016, 09:46
-
- Forum: ✎✎ Lycée
- Sujet: Logarithme neperien
- Réponses: 35
- Vues: 1042
anthony_unac a écrit:Non ! x=0.9 ne convient pas (vous pouvez essayer en réinjectant cette valeur dans l'inéquation).
Pourriez vous m'expliquer pourquoi ?
Bonjour,
x ne convient pas car ln ne peut pas etre négative
ln(x-1)
= ln(-0,1)
- par achoum
- 04 Sep 2016, 09:24
-
- Forum: ✎✎ Lycée
- Sujet: Logarithme neperien
- Réponses: 35
- Vues: 1042
Bonjour, Peut être que vous cherchez trop vite la solution en brûlant les étapes alors voici ce que je vous propose : Résoudre la même inéquation en conservant que le premier terme ln(x-1) donc si je conserve ln(x-1) ln(x-1)<1 x-1<e x<e+1 Aussi ce serait pas mal, par simple respect, comme j...
- par achoum
- 04 Sep 2016, 09:22
-
- Forum: ✎✎ Lycée
- Sujet: Logarithme neperien
- Réponses: 35
- Vues: 1042
anthony_unac a écrit:Oui, c'est très bien concernant la partie calculatoire mais si votre solution est juste alors x=0.9 convient non ?
oui x=0,9 convient
- par achoum
- 03 Sep 2016, 20:41
-
- Forum: ✎✎ Lycée
- Sujet: Logarithme neperien
- Réponses: 35
- Vues: 1042
anthony_unac a écrit:Bonjour,
Peut être que vous cherchez trop vite la solution en brûlant les étapes alors voici ce que je vous propose :
Résoudre la même inéquation en conservant que le premier terme
)
donc si je conserve ln(x-1)
ln(x-1)<1
x-1<e
x<e+1
- par achoum
- 03 Sep 2016, 19:24
-
- Forum: ✎✎ Lycée
- Sujet: Logarithme neperien
- Réponses: 35
- Vues: 1042
Bonjour, Je suis bloqué à une question: énoncé: Résoudre l'inéquation suivante: ln(x-1) - 2ln(x) + ln(x+1) <1 avec l'exponentielle cela donne: x-1 - x²+x+1<e 2x- x²<e Mais apres suis bloquer Aidez moi svp Merci d'avance
- par achoum
- 03 Sep 2016, 18:41
-
- Forum: ✎✎ Lycée
- Sujet: Logarithme neperien
- Réponses: 35
- Vues: 1042
convient puisqu'il appartient à l'intervalle
n'a de sens que si
est positif (et c'était la mise en garde de Lostounet)