27 résultats trouvés
Revenir à la recherche avancée
zygomatique a écrit:salut
la définition de l'ensemble H n'est pas compréhensible ...
C'est tout ce qui est écrit dans mon cahier de cours

- par Yasmiiine
- 29 Juil 2017, 11:36
-
- Forum: ✯✎ Supérieur
- Sujet: Théorème de Cantor-Bernstein
- Réponses: 5
- Vues: 804
Bonjour,je n'arrive pas à comprendre la démonstration du théorème de Cantor-Bernstein: Commençons par son début : Soit f une application injective de E vers F et g injective de F vers E , On pose : h=gof Et soit H un ensemble tel que : H= \left\{M\subseteq E:M \supseteq R\bigcup{h(M)} \right...
- par Yasmiiine
- 28 Juil 2017, 16:24
-
- Forum: ✯✎ Supérieur
- Sujet: Théorème de Cantor-Bernstein
- Réponses: 5
- Vues: 804
Alors : Supposons que U \notin A , on sait que : A= \bar{A} \Leftrightarrow \bar{A} \subset A , \bar{A} n'est pas inclus dans A donc il existe U \in \bar{A} , U \notin A U \in \bar{A} \Rightarrow Quelque soit r>0 , B(U,r) \bigcap{A}\neq \phi Il existe U' \in A ; d(U;U')< r et après ? c'est juste au ...
- par Yasmiiine
- 21 Juil 2017, 18:19
-
- Forum: ✯✎ Supérieur
- Sujet: Espace métrique
- Réponses: 6
- Vues: 284
Bonjour, Montre que le complémentaire de A est ouvert. Pourquoi ainsi c'est plus simple, car on définie les fermées à partir de ouverts, donc ce que tu connais vraiment ce sont les ouverts. Bonne journée. C'est ce que j'allais montrer au début mais le complémentaire de A est ouvert cela veut dire q...
- par Yasmiiine
- 21 Juil 2017, 15:09
-
- Forum: ✯✎ Supérieur
- Sujet: Espace métrique
- Réponses: 6
- Vues: 284
Bonjour,j'arrive pas à démontrer ce théorème,un peu d'aide s'il vous plait? Soit (E,d) un espace métrique, A \subset E , A \neq ∅ A fermé dans E \Leftrightarrow Pour toute suite convergente (Un) de A vers U dans E ; U \in A Alors,pour la première (normalement c'est bon ?) : A fermé dans E \Rightarro...
- par Yasmiiine
- 21 Juil 2017, 13:55
-
- Forum: ✯✎ Supérieur
- Sujet: Espace métrique
- Réponses: 6
- Vues: 284
Salut tout dépend de la définition que tu prends. Si tu considères qu'un ensemble est dénombrable s'il s'injecte dans les entiers alors tout ensemble fini est dénombrable (intuitivement un ensemble dénombrable est un ensemble dans lequel tu peux "numéroter" les éléments). Un ensemble non-...
- par Yasmiiine
- 19 Juil 2017, 15:36
-
- Forum: ✯✎ Supérieur
- Sujet: Ensemble dénombrable
- Réponses: 2
- Vues: 330
Bonjour,
Je voudrai savoir si chaque ensemble dénombrable est un ensemble infini ? Et comment un ensemble non-dénombrable peut être fini ? Une démonstration ou des exemples s'il vous plait ?
- par Yasmiiine
- 19 Juil 2017, 15:17
-
- Forum: ✯✎ Supérieur
- Sujet: Ensemble dénombrable
- Réponses: 2
- Vues: 330
Pardons je voulais dire de l'étape 3 à 4, Oui,je connais bien ces lemmes mais pourquoi d(x;y) \leq 2 M Diam(A)=sup_{x \in A,y \in A} \,d(x;y) \leq 2M Si c'était l'inf j'aurais compris mais c'est bien le sup Merci beaucoup pour votre aide 2M est un majorant des d(x;y) sup d(x...
- par Yasmiiine
- 13 Juil 2017, 16:19
-
- Forum: ✯✎ Supérieur
- Sujet: Diamètre (espace métrique)
- Réponses: 10
- Vues: 1466
il y a deux lemmes à connaitre par coeur lemme1 : si E est un borné de l'e.métrique (X;d) pour tout x,y \in E \qquad d(x;y) \leq Diam(E) lemme2: soient a t b deux réels si pour tout epsilon >0 \, \qquad a \leq b + \epsilon alors a \leq b Pardons je voulais dire de l'étape 3 à 4, Oui...
- par Yasmiiine
- 12 Juil 2017, 16:19
-
- Forum: ✯✎ Supérieur
- Sujet: Diamètre (espace métrique)
- Réponses: 10
- Vues: 1466
on note \bar{A} l'adhérence de A pour la (2) Diam(A) \leq Diam(\bar{A}) car A \subset \bar{A} soit x,y \in \bar{A} Pour tout epsilon>0, Il existe x_0,y_0 \in A tel que d(x,x_0) \leq \epsilon et d(y,y_0) \leq \epsilon d(x,y) \leq d(x,x_0)+d(x_0,y_0...
- par Yasmiiine
- 12 Juil 2017, 15:49
-
- Forum: ✯✎ Supérieur
- Sujet: Diamètre (espace métrique)
- Réponses: 10
- Vues: 1466
pour la (1) A bornée il existe x_0,M>0 tels que A \subset \bar{B}(x_0,M) pour x,y appartenant à A: d(x;y) \leq d(x;x_0)+d(x_0,y) \leq M+M d(x;y) \leq 2 M Diam(A)=sup_{x \in A,y \in A} \,d(x;y) \leq 2M Merci beaucoup c'est plus clair maintenant...
- par Yasmiiine
- 12 Juil 2017, 15:19
-
- Forum: ✯✎ Supérieur
- Sujet: Diamètre (espace métrique)
- Réponses: 10
- Vues: 1466
Bonsoir,j'ai des difficultés avec les espaces métrique..Aidez moi s'il vous plait!! J'arrive pas à comprendre ces deux démonstrations : 1- A est borné \Rightarrow son diamètre est fini Démonstration : Si A est borné alors il existe une boule B(x,M) tq : A \subset B(x,M) c'est à dire : Diam(A) \leq 2...
- par Yasmiiine
- 11 Juil 2017, 20:14
-
- Forum: ✯✎ Supérieur
- Sujet: Diamètre (espace métrique)
- Réponses: 10
- Vues: 1466
Merciiiii beaucoup pour vos méthodes ,une autre question ; Vous faites comment pour écrire les exponentiel et les fractions ?
- par Yasmiiine
- 10 Sep 2016, 17:32
-
- Forum: ✯✎ Supérieur
- Sujet: Intégral
- Réponses: 13
- Vues: 327
Bonjour,j'arrive pas à calculer :
 -1/\exp (2x)+1)
J'ai changé de variable :

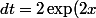 dx)

ça donne :
 dt)
Je n'ai pas d'idées..J'ai essayé mais rien
Merci d'avance
- par Yasmiiine
- 10 Sep 2016, 13:13
-
- Forum: ✯✎ Supérieur
- Sujet: Intégral
- Réponses: 13
- Vues: 327
Bonjour, Si u_n convergeait , sa limite serait -1 , mais comme elle ne converge pas sa limite n'est pas -1 : ici vous avez trouvé qu'elle divergeait vers +\infty . On a : u_n converge \Rightarrow \lim_{n\rightarrow +\infty} u_n = -1 , cette proposition est fausse seulement si u_n converge et \lim_{...
- par Yasmiiine
- 26 Aoû 2016, 14:37
-
- Forum: ✯✎ Supérieur
- Sujet: Suites
- Réponses: 8
- Vues: 330
salut et alors ? as-tu répondu à la question a/ ? as-tu répondu à la question b/ ? Oui,j'ai trouvé l=-1 Et j'ai vérifié que Un est positive ( raisonnement par récurrence ),et en fait il y aussi deux autres questions : c) Montrer que Un est monotone : J'ai trouvé Un+1 -Un positive donc oui elle est ...
- par Yasmiiine
- 26 Aoû 2016, 12:27
-
- Forum: ✯✎ Supérieur
- Sujet: Suites
- Réponses: 8
- Vues: 330
zygomatique a écrit:salut
et si tu donnais l'énoncé exact au lieu de tourner autour du pot !!!
- par Yasmiiine
- 26 Aoû 2016, 10:43
-
- Forum: ✯✎ Supérieur
- Sujet: Suites
- Réponses: 8
- Vues: 330
Bonjour, une suite u_n converge vers -1 , veut dire qu'il existe une infinité de termes de la suite qui se trouvent dans un voisinage de -1 aussi petit soit-il , mais on peut avoir les premiers termes de la suite positifs : \forall \epsilon > 0 , \exists N\in \mathbb N , \forall n \in \mathbb N : n...
- par Yasmiiine
- 26 Aoû 2016, 10:08
-
- Forum: ✯✎ Supérieur
- Sujet: Suites
- Réponses: 8
- Vues: 330
