256 résultats trouvés
Revenir à la recherche avancée
Re: théorème de Ménélaus
pour avoir les coordonnées du point P si on se place dans un repère (A;\overrightarrow{AB};\overrightarrow{AC}) alors \overrightarrow{AB} = x. \overrightarrow{AB} + x. \overrightarrow{AC} donc les coordonnées de vecteur \overrightarrow{AM}=\frac{1}{1 - c}\overrightarrow{AB}-\frac{c}{1 - c}\o...
- 25 Nov 2017, 17:27
- Forum: ✎✎ Lycée
- Sujet: théorème de Ménélaus
- Réponses: 76
- Vues: 2740
Re: théorème de Ménélaus
chouette !
- 25 Nov 2017, 17:11
- Forum: ✎✎ Lycée
- Sujet: théorème de Ménélaus
- Réponses: 76
- Vues: 2740
Re: théorème de Ménélaus
salut Lostounet
j'espère que tu passes un bel après - midi !
c'est quoi les partiels ?
j'espère que tu passes un bel après - midi !
c'est quoi les partiels ?
- 25 Nov 2017, 16:41
- Forum: ✎✎ Lycée
- Sujet: théorème de Ménélaus
- Réponses: 76
- Vues: 2740
Re: théorème de Ménélaus
il y a aussi une belle faute d'orthographe : j'ai écrit sont opposé
- 25 Nov 2017, 16:04
- Forum: ✎✎ Lycée
- Sujet: théorème de Ménélaus
- Réponses: 76
- Vues: 2740
Re: théorème de Ménélaus
Salut Lostounet
( comment vas - tu ? )
Peux tu m'expliquer ? s'il te plait
( comment vas - tu ? )
Peux tu m'expliquer ? s'il te plait
- 25 Nov 2017, 16:03
- Forum: ✎✎ Lycée
- Sujet: théorème de Ménélaus
- Réponses: 76
- Vues: 2740
Re: théorème de Ménélaus
Salut Je viens de voir ton message seulement maintenant ( j'aurais du te répondre bien avant !! ) j'avais trouvé \overrightarrow{MA}=-\frac{1}{1-c}\overrightarrow{AB}+\frac{c}{1 - c}\overrightarrow{AC} et pour trouver AM : je dois prendre sont opposé :( l'opposé de MA ) c'est à dire \overrightarrow{...
- 24 Nov 2017, 23:13
- Forum: ✎✎ Lycée
- Sujet: théorème de Ménélaus
- Réponses: 76
- Vues: 2740
Re: montrer que les points B, D et Q sont alignés
Bonjour et merci de m'avoir répondu
en posant AP = x
le point P a pour abscisse x et 0 pour ordonnée
soit P ( x;0)
--------------------------
Pour le point R
il faut partir de AP = RD donc RD =x
en posant AP = x
le point P a pour abscisse x et 0 pour ordonnée
soit P ( x;0)
--------------------------
Pour le point R
il faut partir de AP = RD donc RD =x
- 22 Nov 2017, 14:52
- Forum: ✎✎ Lycée
- Sujet: montrer que les points B, D et Q sont alignés
- Réponses: 4
- Vues: 893
Re: montrer que les points B, D et Q sont alignés
comme QA = -RP
et avec A(0;0)
P(1;0)
R(0;1)
j'ai ensuite fait un système de 2 équations :
0 - xQ = -(1 - 0)
-xQ = -1
soir xQ = 1
0 - yQ = - (0 - 1)
-yQ = 1 soit yQ = - 1
et avec A(0;0)
P(1;0)
R(0;1)
j'ai ensuite fait un système de 2 équations :
0 - xQ = -(1 - 0)
-xQ = -1
soir xQ = 1
0 - yQ = - (0 - 1)
-yQ = 1 soit yQ = - 1
- 21 Nov 2017, 22:06
- Forum: ✎✎ Lycée
- Sujet: montrer que les points B, D et Q sont alignés
- Réponses: 4
- Vues: 893
montrer que les points B, D et Q sont alignés
Bonsoir ABCD est un carré P est le point du segment [AB] distincts de A et B. R est le point du segment [AD] tel que DR=AP ensuite, Q est le point tel que APQR est un rectangle Démontrer que les points B,D Q sont alignés (utiliser les 2 méthodes suivantes : Les vecteurs et les coordonnées dans un re...
- 21 Nov 2017, 21:18
- Forum: ✎✎ Lycée
- Sujet: montrer que les points B, D et Q sont alignés
- Réponses: 4
- Vues: 893
Re: théorème de Ménélaus
Bonjour
Quelqu'un pour m'aidez à trouver le vecteur AM ?
s'il vous plait
Quelqu'un pour m'aidez à trouver le vecteur AM ?
s'il vous plait
- 20 Nov 2017, 13:56
- Forum: ✎✎ Lycée
- Sujet: théorème de Ménélaus
- Réponses: 76
- Vues: 2740
Re: théorème de Ménélaus
Pouvez m'aidez à trouver le vecteur AM ?
- 20 Nov 2017, 11:47
- Forum: ✎✎ Lycée
- Sujet: théorème de Ménélaus
- Réponses: 76
- Vues: 2740
Re: théorème de Ménélaus
pour la 3 ) a ) partant de l'égalité donnée : \overrightarrow{MB}=c\overrightarrow{MC} et en introduisant le point A \overrightarrow{MB}=\overrightarrow{MA}+\overrightarrow{AB} et \overrightarrow{MC} =\overrightarrow{MA}+\overrightarrow{AC} donc c\overrightarrow{MC}=c\overrightarrow{MA}+c\overrighta...
- 19 Nov 2017, 23:30
- Forum: ✎✎ Lycée
- Sujet: théorème de Ménélaus
- Réponses: 76
- Vues: 2740
Re: théorème de Ménélaus
Bonsoir 3 ) a ) montrer que \overrightarrow{AM}=\frac{1}{1-c}\overrightarrow{AB}-\frac{c}{1 - c}\overrightarrow{AC} b ) En déduire les coordonnées du point M 4 ) a ) Exprimer le vecteur \overrightarrow{PA} en fonction du vecteur \overrightarrow{AB} b ) En déduire les coordonnées du point P et montre...
- 19 Nov 2017, 23:22
- Forum: ✎✎ Lycée
- Sujet: théorème de Ménélaus
- Réponses: 76
- Vues: 2740
Re: théorème de Ménélaus
oK
Bonsoir Ben ( merci de m'avoir répondu )
et si a = 1 cela veut dire que les vecteurs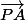 et
et 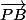 sont égaux ?
sont égaux ?
Bonsoir Ben ( merci de m'avoir répondu )
et si a = 1 cela veut dire que les vecteurs
- 19 Nov 2017, 00:15
- Forum: ✎✎ Lycée
- Sujet: théorème de Ménélaus
- Réponses: 76
- Vues: 2740
Re: théorème de Ménélaus
Bonsoir Pour la question 1 ) les deux vecteurs \overrightarrow{PA} et \overrightarrow{PB} sont colinéaires s'il existe un réel a tel que \overrightarrow{PA}=a\overrightarrow{PB} donc je peux justifier l'existence de ce réel a si les vecteurs sont colinéaires le seul fait qu'ils soient qu'ils aient l...
- 18 Nov 2017, 23:03
- Forum: ✎✎ Lycée
- Sujet: théorème de Ménélaus
- Réponses: 76
- Vues: 2740
Re: théorème de Ménélaus
je ne vois pourquoi les vecteurs MB et MC sont colinéaires ?
- 15 Nov 2017, 15:18
- Forum: ✎✎ Lycée
- Sujet: théorème de Ménélaus
- Réponses: 76
- Vues: 2740
Re: théorème de Ménélaus
Pour que deux vecteurs 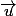 et
et 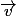 soient colinéaires : il faut un nombre réel k tel que
soient colinéaires : il faut un nombre réel k tel que 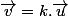
- 15 Nov 2017, 13:04
- Forum: ✎✎ Lycée
- Sujet: théorème de Ménélaus
- Réponses: 76
- Vues: 2740
Re: théorème de Ménélaus
Bonjour Lostounet
il faut terminer la 1 )
je n'arrive pas à démontrer que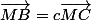
il faut terminer la 1 )
je n'arrive pas à démontrer que
- 15 Nov 2017, 13:02
- Forum: ✎✎ Lycée
- Sujet: théorème de Ménélaus
- Réponses: 76
- Vues: 2740
Re: théorème de Ménélaus
Bonjour Les vecteurs \overrightarrow{PA} et \overrightarrow{PB} sont colinéaires et les vecteurs \overrightarrow{NC} et \overrightarrow{NA} sont également colinéaires Pour les vecteurs \overrightarrow{MB} et \overrightarrow{MC} là je ne vois pas comment démontrer l'existence d'un réel c tel que \ove...
- 15 Nov 2017, 11:36
- Forum: ✎✎ Lycée
- Sujet: théorème de Ménélaus
- Réponses: 76
- Vues: 2740
- 15 Nov 2017, 00:15
- Forum: ✎✎ Lycée
- Sujet: théorème de Ménélaus
- Réponses: 76
- Vues: 2740
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
