33 résultats trouvés
Revenir à la recherche avancée
Re: raccordement equa diff
Salut, On a donc y(t)=\lambda_1 e^{-\frac{1}{t}} pour t\in ]0;+\infty[ et y(t)=\lambda_2 e^{-\frac{1}{t}} pour t\in ]-\infty;0[ . Lorsque t tend vers 0 par valeurs positives, \lim_{t\to 0^+} \lambda_1 e^{-\frac{1}{t}}=0 quelle que soit la valeur de \lambda_1 finie. Or, \lim_{t\to 0^-...
- 12 Jan 2025, 16:06
- Forum: ✯✎ Supérieur
- Sujet: raccordement equa diff
- Réponses: 3
- Vues: 1511
Re: Intégrale impropre
Bonjour, Je pense que l'on peut chercher une primitive de x\to ln(1+x^2) puis de x\to ln(x^2) . Puis on calcule les limites. Je trouve que \int [ln(1+x^2)-ln(x^2)]dx=-xln(x^2)+xln(x^2+1)+2arctan(x) (c'est une primitive). Puis, \lim_{x\to +\inft...
- 21 Juil 2023, 07:22
- Forum: ✯✎ Supérieur
- Sujet: Intégrale impropre
- Réponses: 2
- Vues: 486
Re: Limite chez les complexes
Merci Doraki, j'ai compris là où ça coinçait.
Merci mathelot pour le raisonnement détaillé.
Je posterai une autre limite pour vérifier que j'ai bien compris.
Merci mathelot pour le raisonnement détaillé.
Je posterai une autre limite pour vérifier que j'ai bien compris.
- 23 Jan 2023, 17:30
- Forum: ✯✎ Supérieur
- Sujet: Limite chez les complexes
- Réponses: 4
- Vues: 521
Limite chez les complexes
Bonjour, Je souhaite démontrer, à l'aide de la définition de la limite, que \lim_{z\to 1+2i} f(z)=\sqrt(5} avec f(z)=|z| . L'application f est une application de la variable complexe. Il s'agit donc de démontrer que \forall \epsilon > 0, \exists \eta > 0, \forall z\in \mathbb{C},...
- 22 Jan 2023, 14:27
- Forum: ✯✎ Supérieur
- Sujet: Limite chez les complexes
- Réponses: 4
- Vues: 521
Re: Limite par la définition
Ah mais oui, bien sûr !
Merci Mateo.
Merci Mateo.
- 22 Jan 2023, 06:07
- Forum: ✯✎ Supérieur
- Sujet: Limite par la définition
- Réponses: 3
- Vues: 315
Limite par la définition
Bonjour, Je lis une démonstration du fait que \lim_{x\to 1} (1+\frac{1}{x})=2 à l'aide de la définition avec des epsilons. Je comprends l'ensemble de la preuve, mais un passage me gêne. Il est écrit que l'on peut supposer que \epsilon \in ]0;1[ , car "si l'on peut rendre |1-\frac{1}{x}|...
- 21 Jan 2023, 15:58
- Forum: ✯✎ Supérieur
- Sujet: Limite par la définition
- Réponses: 3
- Vues: 315
Re: fonction
Si tu ne connais pas par cœur les identités remarquables, écris simplement que :
^2=(a-b)(a-b)) puis développe en utilisant la double distributivité.
puis développe en utilisant la double distributivité.
Re: Limite
Il faudrait préciser que 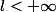 dans le cas d'une suite convergente.
dans le cas d'une suite convergente.
Aussi,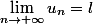 équivaut à
équivaut à 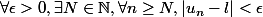 .
.
Aussi,
Re: Question de statistique
Hello, Tu peux résumer ta série par l'étude du couple (médiane,intervalle interquartile) qui robuste par rapport aux valeurs extrêmes. Plus l'intervalle interquartile est grand, plus les valeurs de la série sont dispersées par rapport à la médiane. Pour ton premier exemple, Q_2-Q_1=269-207=62. Cet é...
- 17 Oct 2018, 17:17
- Forum: ⚜ Salon Mathématique
- Sujet: Question de statistique
- Réponses: 2
- Vues: 444
Re: salut j'ai besoin e vous m'aidez
Salut, "Que vous m'aid iez " On peut procéder par substitution en isolant soit X soit Y dans la seconde équation. En reportant dans la première équation, tu obtiendra une équation du second degré, soit en X, soit en Y. Attention à prendre toutes les précautions nécessaires sur les valeurs ...
- 15 Oct 2018, 18:05
- Forum: ✎✎ Lycée
- Sujet: salut j'ai besoin e vous m'aidez
- Réponses: 1
- Vues: 1312
Re: Nouvelle appli iPhone et iPad pour les maths
Salut,
J'étais tombé sur ton application au détour d'un forum, et je l'ai trouvé vraiment utile et aboutie. Bravo pour le boulot !!
Je suis un utilisateur de Windows phone. Est-ce que tu prévois une adaptation ?
Bonne continuation
J'étais tombé sur ton application au détour d'un forum, et je l'ai trouvé vraiment utile et aboutie. Bravo pour le boulot !!
Je suis un utilisateur de Windows phone. Est-ce que tu prévois une adaptation ?
Bonne continuation
- 30 Aoû 2016, 22:08
- Forum: ✯✎ Supérieur
- Sujet: Nouvelle appli iPhone et iPad pour les maths
- Réponses: 4
- Vues: 1567
Re: Limites
Je t'en prie ^^
Re: Intégrale de Wallis
Salut,
Encadre des formules avec les balises LaTeX
Quand on travailles avec des intégrales de Wallis, bien souvent on démontre pas mal de relations avec une IPP.
Encadre des formules avec les balises LaTeX
Quand on travailles avec des intégrales de Wallis, bien souvent on démontre pas mal de relations avec une IPP.
- 28 Aoû 2016, 22:30
- Forum: ✯✎ Supérieur
- Sujet: Intégrale de Wallis
- Réponses: 9
- Vues: 735
Re: Limites
Salut, Je propose ceci, en remarquant que sin(x)=\Big(\sqrt{sin(x)}\Big)^2 et en appelant g(x) la quantité dont on cherche la limite : g(x)=\Big(\sqrt{\dfrac{1}{sin(x)}}-2\Big)^2\Big(\sqrt{sin(x)}\Big)^2=\Big(\dfrac{\sqrt{si...
Re: Étape d'un calcul
Bon je me suis pas fais comprendre alors. Pour répondre à la consigne il faut faire Un+1-Un, c'est ce que j'ai fais sauf que j'ai bloqué à une étape j'ai regardé la correction, & il y avait écrit ce que je vous ai indiqué! Alors je comprend pas pourquoi vous me ressortez (a+b)(a-b), puisque dan...
- 27 Aoû 2016, 12:43
- Forum: ✎✎ Lycée
- Sujet: Étape d'un calcul
- Réponses: 17
- Vues: 975
Re: Étape d'un calcul
Et donc, quel est ton raisonnement ... Ça n'avance pas hein !
Sinon, pour revenir à la question de base, il suffit de montrer que :
\big(\sqrt{n+1}+\sqrt{n}\big)=1)
On te l'a dit, applique simplement l'identité(a+b )=a^2-b^2)
Sinon, pour revenir à la question de base, il suffit de montrer que :
On te l'a dit, applique simplement l'identité
- 27 Aoû 2016, 10:37
- Forum: ✎✎ Lycée
- Sujet: Étape d'un calcul
- Réponses: 17
- Vues: 975
Re: Étape d'un calcul
Donne-nous l'énoncé exact, ça sera tellement plus simple !!!
- 26 Aoû 2016, 21:08
- Forum: ✎✎ Lycée
- Sujet: Étape d'un calcul
- Réponses: 17
- Vues: 975
Re: Étape d'un calcul
Je ne comprend pas vos réponses, enfaite si ça peut aider c'est une fraction: ((Rac(n+1)-Rac(n))(Rac(n+1)-rac(n)))/Rac(n+1)+Rac(n) Le résultat étant: 1/Rac(n+1)+Rac(n) Je ne comprends pas ta question. Tout t'a été expliqué ! Il y a une erreur au numérateur. C'est l'expression que j'ai donnée dans m...
- 26 Aoû 2016, 17:15
- Forum: ✎✎ Lycée
- Sujet: Étape d'un calcul
- Réponses: 17
- Vues: 975
Re: Equation trigonométrique TS
Salut,
=2cos^2(X)) pour tout
pour tout 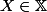 .
.
En prenant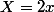 , avec
, avec 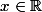 , tu obtiens :
, tu obtiens :
=2cos^2(2x))
D'où+cos(4x)=2cos^2(2x)+cos(2x))
En prenant
D'où
- 26 Aoû 2016, 14:42
- Forum: ✎✎ Lycée
- Sujet: Equation trigonométrique TS
- Réponses: 3
- Vues: 370
Re: Étape d'un calcul
Oups désolé, j'ai cru à une fraction ...
Dans ton premier post, c'est la même quantité dans le membre de droite que dans celui de gauche.
Il faut considérer\big(\sqrt{n+1}+\sqrt{n}\big)) , puis suivre l'indication de beagle.
, puis suivre l'indication de beagle.
Dans ton premier post, c'est la même quantité dans le membre de droite que dans celui de gauche.
Il faut considérer
- 26 Aoû 2016, 14:08
- Forum: ✎✎ Lycée
- Sujet: Étape d'un calcul
- Réponses: 17
- Vues: 975
- 33 résultats trouvés - Page 1 sur 2 • 1, 2
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
