Forum de Mathématiques: Maths-Forum

Bonjour, je dois résoudre cette équation qui admet, s'il y a, des solutions entières : x^y+y^x=1 . J'ai trouvé des solutions évidentes (x,y)=(0,y),(x,0) . Je ne sais pas s'il en existe d'autres. En fait en travaillant dans N , on s'aperçoit vite que ce sont les seules solutio...

Bonjour, en cours de résolution d'un problème de géométrie, je m'aperçois que je peux construire des droites supplémentaires pour faciliter justement sa résolution. Je voudrais donc savoir quand faut-il, en général, faire des constructions supplémentaires. Ensuite, comment savoir où en faire ? Je vo...

Ah ok. Et c'est vraiment trop compliqué co3 ?

Le sommet se trouve sur l'axe y, le graphique est symétrique à cette axe.

Bonjour, je voudrais comprendre la molécule 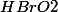. En effet, pourquoi a-t-elle des électrons libres ? De même pour 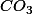? Comment ces atomes peuvent-ils être liés ? Ne sont-ils pas de la sorte plus instables ?

Que voulez-vous dire ?

Ok. Un grand merci à vous.

PS: une possibilité serait en fait que la fonction (parabolique) admette b=0 comme proposé ^^

Oui, je suis d'accord avec vous, j'essaye juste de comprendre. En fait, l'équation est l'équation du mouvement uniformément accéléré, donc b n'est pas nul. x_t(t)=x_0+v_0t+\frac{at^2}{2} . En traçant ce graphique en fonction de t², je suis censé tomber sur une droite. Je ne sais pas ... Est-...

Dans un exercice, je dois prouver qu'un graphique est une fonction du second degré. Pour ce faire, mon professeur m'a proposé de tracer le même graphique en fonction de x² : si la fonction est linéaire, c'est une fonction du second degré.

Bonsoir, en fait ma question vient de ceci:
"Trouver l'expression analytique de f(x) en fonction de x² tel que f(x)=ax²+bx+c."

Plus simplement, tracer le graphique de f(x)=3x²+5x+2 en fonction de x² et je dois arriver à une droite.

Bonsoir, il est claire qu'une fonction peut être définie comme suivant : f: x \rightarrow x^2+1: R \rightarrow R . Je me demande donc ce que signifie : f: 2x^2+1 \rightarrow x^3+2x+4: R \rightarrow R par exemple. Est-ce possible de trouver la fonction ? ( f: x\rightarrow f(x) ) J'aimerais de...

J'ai compris, enfin ! Merci de ton aide !


PS: c'est vrai que concernant les cours de logique, je n'en ai jamais eu ...

Dans l'exemple, je crois que c'est parce que on a à faire à deux équation différentes P(x)=0 et x=0 qu'on fusionne ensemble, or les x ne valent pas forcément la meme chose (différent ensemble de solution(s) .

Bien que tu expliques bien, je ne suis pas sûr de comprendre, ni même l'exemple (que je te remercie d'avoir injecté dans réponse).
Je ne sais pas comment il faudrait faire pour que je comprenne ...

Bonsoir, pour résoudre une équation fonctionnelle, il est logique d'utiliser la substitution. Par exemple, je pourrais remplacer des inconnues par certaines valeurs pour obtenir des informations utiles et ainsi trouver au final les (la) solution(s) de l‘équation. Toutefois, il arrive que certaines f...

Oui, cela marche. Merci.

Ah oui effectivement. J'aurais une autre demande: quelqu'un pourrait m'expliquer le principe du vecteur vitesse instantanée ? En utilisant un exemple.

Bonsoir, après lecture de mon cours, je ne sais pas au final si "changer direction", c'est modifier la vitesse. D'après moi, quand je change de direction, la vitesse peut rester constante. Toutefois, en dessinant 2 vecteurs vitesses à des moments différents, je peux tracer le vecteur chang...

Bonsoir, oui je comprends. En effet, quand je dis que quelque soient les réels x, racine de x est un réel , si je prends x=2 j'arrive à un résultat vrai,or la proposition est fausse ... ^^
Merci pour vos efforts !

Ok. Alors prouve-moi que c'est cette méthode qui fonctionne et pas une autre ...