 , mais je voulais dire localement compacte.
, mais je voulais dire localement compacte.16 résultats trouvés
Revenir à la recherche avancée
Re: Espace des fonctions continues à support compact
dsl  , mais je voulais dire localement compacte.
, mais je voulais dire localement compacte.
 , mais je voulais dire localement compacte.
, mais je voulais dire localement compacte.- 21 Avr 2017, 10:05
- Forum: ✯✎ Supérieur
- Sujet: Espace des fonctions continues à support compact
- Réponses: 11
- Vues: 1152
Re: Espace des fonctions continues à support compact
oui, Merci beaucoup.
J` ai une autre question. Dans le cas ou est relative compact, l'adhérence de
est relative compact, l'adhérence de ) est-il aussi
est-il aussi ) ?
?
J` ai une autre question. Dans le cas ou
- 19 Avr 2017, 16:40
- Forum: ✯✎ Supérieur
- Sujet: Espace des fonctions continues à support compact
- Réponses: 11
- Vues: 1152
Re: Espace des fonctions continues à support compact
c`est facile a voir bien sur dans le cas ou notre espace  est un espace compact.
est un espace compact.
En effet, soit) alors supp(f)
alors supp(f) 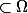 et il est fermé est par suite le support de la fonction f est un compact. et donc
et il est fermé est par suite le support de la fonction f est un compact. et donc )
En effet, soit
- 19 Avr 2017, 15:44
- Forum: ✯✎ Supérieur
- Sujet: Espace des fonctions continues à support compact
- Réponses: 11
- Vues: 1152
Re: Espace des fonctions continues à support compact
Salut ben,
il est facile de voir que \subset C_K(\Omega)) et par suite
et par suite  = C_b (\Omega)) , Mais comment peux je monter que
, Mais comment peux je monter que }=C_b (\Omega)) ?(il suffit de montrer que
?(il suffit de montrer que ) est un ferme)?
est un ferme)?
il est facile de voir que
- 19 Avr 2017, 13:39
- Forum: ✯✎ Supérieur
- Sujet: Espace des fonctions continues à support compact
- Réponses: 11
- Vues: 1152
Re: Espace des fonctions continues à support compact
T'as raison Ben, dans mon cas,  est une espace topologique separée
est une espace topologique separée
- 12 Avr 2017, 10:33
- Forum: ✯✎ Supérieur
- Sujet: Espace des fonctions continues à support compact
- Réponses: 11
- Vues: 1152
Espace des fonctions continues à support compact
Bonjour, je veux determiner la fermeture de C_K(\Omega) (l'espace des fonctions continues à support compact) dans ( C_b(\Omega), ||.||_{\Omega} ),où C_b(\Omega) est l'espace des fonctions continues borne et ||.||_{\Omega}= sup_{\omega \in \Omega} |f(\omega)| . Sachant...
- 12 Avr 2017, 10:05
- Forum: ✯✎ Supérieur
- Sujet: Espace des fonctions continues à support compact
- Réponses: 11
- Vues: 1152
fonction continue
Bonjour,
j'ai une question.
Soit P la fonction definit comme suit:
\big))
_n) est une suite quelconque.
est une suite quelconque.
la fonction P est elle continue?
j'ai une question.
Soit P la fonction definit comme suit:
la fonction P est elle continue?
- 23 Aoû 2016, 12:29
- Forum: ✯✎ Supérieur
- Sujet: fonction continue
- Réponses: 1
- Vues: 207
mesure de probabilité
bonjour tout le monde,
j'ai une question,
Une mesure qui a une support
qui a une support  et
et = 1) , est il une mesure de probabilité?
, est il une mesure de probabilité?
merci
j'ai une question,
Une mesure
merci
- 25 Juil 2016, 16:46
- Forum: ✯✎ Supérieur
- Sujet: mesure de probabilité
- Réponses: 1
- Vues: 385
Re: serie convergente
Merci beaucoup samoufar pour ton aide 
- 09 Juin 2016, 09:56
- Forum: ✯✎ Supérieur
- Sujet: serie convergente
- Réponses: 13
- Vues: 734
Re: serie convergente
Merci beaucoup pour ton aide  , Mais je n'ai pas compris une chose dans la deuxieme etape: comment peut on montrer que la suite est convergente? et comment je peux utiliser la suite
, Mais je n'ai pas compris une chose dans la deuxieme etape: comment peut on montrer que la suite est convergente? et comment je peux utiliser la suite  .. je sais que cette suite est decroissante et que
.. je sais que cette suite est decroissante et que 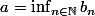
- 08 Juin 2016, 12:20
- Forum: ✯✎ Supérieur
- Sujet: serie convergente
- Réponses: 13
- Vues: 734
Re: serie convergente
peut tu m'expliquer plus?,
voila comment je peut voire la limite superieure,
 .
.
voila comment je peut voire la limite superieure,
- 07 Juin 2016, 16:05
- Forum: ✯✎ Supérieur
- Sujet: serie convergente
- Réponses: 13
- Vues: 734
Re: serie convergente
Merci  ,
,
J'ai une autre question,
si
reste le resultat encore vrai?
J'ai une autre question,
si
reste le resultat encore vrai?
- 07 Juin 2016, 14:10
- Forum: ✯✎ Supérieur
- Sujet: serie convergente
- Réponses: 13
- Vues: 734
Re: serie convergente
on a s > a alors il existe \eta > 0 ; s - a \geq \eta pour \xi = s - a - \eta, \exists N \succ 1 ; a_n - a \leq s - a - \eta et par consequence a_n - s \prec - \eta par suite \sum_{n \geq N} \exp \left(n\left(a_n -s \right) \right) \leq \sum_{n \geq N} \exp \left(-n \eta} \right&...
- 07 Juin 2016, 09:34
- Forum: ✯✎ Supérieur
- Sujet: serie convergente
- Réponses: 13
- Vues: 734
Re: serie convergente
merci pour ton aide, j'essaierai de trouver cette 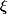
- 07 Juin 2016, 08:08
- Forum: ✯✎ Supérieur
- Sujet: serie convergente
- Réponses: 13
- Vues: 734
Re: serie convergente
pour \xi \geq 0, \exists N\geq 0; \forall n \geq N, a_n -s \leq \xi alors \sum_{n \geq 1} \exp \left(n\left(a_n -s \right) \right)= \sum_{n \prec N} \exp \left(n\left(a_n -s \right) \right) + \sum_{n \geq N} \exp \left(n\left(a_n -s \right) \right) et ...
- 06 Juin 2016, 15:21
- Forum: ✯✎ Supérieur
- Sujet: serie convergente
- Réponses: 13
- Vues: 734
serie convergente
bonjour tout le monde,
j'ai une question concernant les series.
soit une suite qui converge vers a.
une suite qui converge vers a.
et soit s > a,
est ce que la serie
 \right)) est converege ?
est converege ?
je pense que oui, pouviez vous m'aider?
j'ai une question concernant les series.
soit
et soit s > a,
est ce que la serie
je pense que oui, pouviez vous m'aider?
- 06 Juin 2016, 14:45
- Forum: ✯✎ Supérieur
- Sujet: serie convergente
- Réponses: 13
- Vues: 734
- 16 résultats trouvés - Page 1 sur 1
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
