8 résultats trouvés
Revenir à la recherche avancée
Re: les integrales curvilignes et l'analyse vectorielle
Oui je sais merci
- 01 Juin 2016, 18:17
- Forum: ✯✎ Supérieur
- Sujet: les integrales curvilignes et l'analyse vectorielle
- Réponses: 13
- Vues: 620
- 01 Juin 2016, 16:19
- Forum: ✯✎ Supérieur
- Sujet: les integrales curvilignes et l'analyse vectorielle
- Réponses: 13
- Vues: 620
Re: les integrales curvilignes et l'analyse vectorielle
et pour la 2eme comme j'ai les bornes de t je calcule r(-1) et r(1) avec l'expression donnée et de la j'obtiens les points A et B et je peux donc évaluer l'intégrale facilement avec f(B) - f(A) c'est ça?
- 01 Juin 2016, 16:14
- Forum: ✯✎ Supérieur
- Sujet: les integrales curvilignes et l'analyse vectorielle
- Réponses: 13
- Vues: 620
Re: les integrales curvilignes et l'analyse vectorielle
j'ai compris mon erreur en fait j'ai tout additionné après avoir fait les intégrales et c'est faux en faisant le chemin inverse en effet j'aurais du verifié, c'est bien ça? 
- 01 Juin 2016, 16:09
- Forum: ✯✎ Supérieur
- Sujet: les integrales curvilignes et l'analyse vectorielle
- Réponses: 13
- Vues: 620
- 01 Juin 2016, 16:03
- Forum: ✯✎ Supérieur
- Sujet: les integrales curvilignes et l'analyse vectorielle
- Réponses: 13
- Vues: 620
Re: les integrales curvilignes et l'analyse vectorielle
Est-ce que tu as vérifié pour le potentiel que tu as calculé que cette relation entre et est bien satisfaite ? J'ai pas trop compris ce que cela veut dire 2°) Si tu as bien trouvé un potentiel pour le champ , tu devrais savoir que l'intégrale curviligne de le long d'un chemin ne dépend que des valeu...
- 01 Juin 2016, 15:31
- Forum: ✯✎ Supérieur
- Sujet: les integrales curvilignes et l'analyse vectorielle
- Réponses: 13
- Vues: 620
Re: les integrales curvilignes et l'analyse vectorielle
Alors pour la 1 j'ai posé Fx= 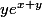
Fy= e^{x+y} + 2y)
Fz= -2z
et du coup aprés j'ai posé pour chacun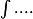 selon dx pour Fx, dy pour Fy et dz pour Fz
selon dx pour Fx, dy pour Fy et dz pour Fz
est ce que la méthode est correcte?
Fy=
Fz= -2z
et du coup aprés j'ai posé pour chacun
est ce que la méthode est correcte?
- 01 Juin 2016, 15:26
- Forum: ✯✎ Supérieur
- Sujet: les integrales curvilignes et l'analyse vectorielle
- Réponses: 13
- Vues: 620
les integrales curvilignes et l'analyse vectorielle
maths.PNG Bonjour, j'ai un exercice à faire dont la consigne est en pièce jointe et si quelqu'un peut m'aider à y voir un peu plus clair ce ne serait pas de refus :p j'aimerais savoir si j'ai la bonne méthode s'il vous plait 1) pour trouver le champ de potentiel j'ai integré la composante du vecteu...
- 31 Mai 2016, 04:50
- Forum: ✯✎ Supérieur
- Sujet: les integrales curvilignes et l'analyse vectorielle
- Réponses: 13
- Vues: 620
- 8 résultats trouvés - Page 1 sur 1
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
