Forum de Mathématiques: Maths-Forum

Bonsoir pouvez vous m aider a comprendre

algo fibo
var f1,f2,temp ,n,i : entier
f1=1
f2=1
i =3
saisir n
si n >2 alors

repeter

temp=f1+f2
f2=f1
f1= temp
i=i+1
jusqu a i>n

Merci à tous pour votre aide. J'ai été reçu pour ma formation le plus dur commence je posterai à nouveau si j'ai des difficultés.

merci Laetidom je crois que c'est bon pour moi !

Ok je comprends mais pour exemple quand on développe (2x-1)² on à bien une identitée de type (a-b)² ce que je n'arrive pas à faire c'est choisir le signe de b quand on la développe. 4x²-2*2x* 1ou -1+1² ou (-1)² voilà ou je bloque c'est tout bete mais je fais des erreurs a cause de ca . Et la pour te...

Comme je te l'ai dit une fois, tu peux prendre a = 2x et b = 1 et dans ce cas c'est la forme (a - b)^2 = (2x - 1)^2 = 4x^2 - 2*(2x)*1 + 1 ou bien tu peux prendre a = 2x et b = -1 et dans ce cas, c'est de la forme (a + b)^2 = (2x + (- 1))^2 = 4x^2 + 2*(2x)*(-1) + 1 = 4x^2 - 4x + 1 Mais dans les deux...

Tu peux prendre (-1), tu peux prendre (+10) tu peux prendre (ma tante) peu importe. Mais on avait -x^2 + 2x - 1 et toi tu voulais (x^2 ...). le seul moyen d'y parvenir c'est de faire *(-1) pour virer le signe - devant x^2 pour pouvoir factoriser Ok merci de ton aide lostounet. Une question simple m...

Tu ne sais pas que, dans une équation, on peut multiplier et diviser les deux cotés par un même nombre? Et tu ne connais pas la règle de distributivité suivante ? Si au supermarket j'achète deux sachets, avec dans chaque sachet 1 pomme et une poire, alors en tout j'ai: DEUX(Pomme + Poire) c'est DEU...

J'aimerai comprendre comment arriver a ce résultat mois je trouve -x²+2x+3=4 -x²+2x-1=0 x²+2x+1²=0 erreur ici Comment tu passes de -x^2 + 2x - 1 = 0 à la ligne suivante? tu multiplies par (-1) les deux membres de l'équation et cela te donne: (-1)*[-x^2 + 2x - 1] = (-1)*0 x^2 - 2x + 1 = 0 Et ça c'es...

Salut ! Réécris ton équation sous la forme x^2+2ax+b =0 , où a et b sont deux réels que tu préciseras. Ensuite, remarque que puisque x^2+2ax+a^2 = (x+a)^2 , on a x^2+2ax = (x+a)^2-a^2 . Ainsi, résoudre x^2+2ax+b =0 revient à résoudre (x+a)^2-a^2+b =0 . ;) Salut merci de ta r...

Bonsoir.

Quelqu'un peut m'aider a factoriser en utilisant les identitées remarquable l'équation suivante je ne m'en sors pas a cause des signes moins.

-x²+2x+3=4

Merci

comme ca je crois je m'etais trompé dans les sisignes

2²-(x+1)=0
(2-(x+1)) (2+(x+1))=0
(2-x-1)(2+x+1)=0
(-x+1)(x+3)=0
donc -x=-1 x=1

et x = -3

Lostounet a écrit:Hey Cidou,

Crois-moi, pour progresser il faut vraiment que tu essayes de faire un raisonnement d'écrire

Tu n'apprendras qu'en faisant des erreurs..

ok merci pour le conseil.

Peut on développer l'équation suivante.

4-(x+1)²=0

avec l'identité remarquable a²-b²

je n'arrive pas au même résultat avec la forme x²=a

Merci.

Simple mais efficace merci beaucoup Lostounet.

(2x-6)2x=0
les réponse sont x= 0 ou x=3

comment trouver 3 je ne comprend pas ?

Peux tu développer stp.

dans le corrigé ces ecrit

x+1+6=2+3x+5

Tu peux développer l'opération stp

Bonjour
Pouvez vous m'aider à développer l'équation suivante:

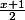+3 =1+

Merci.

Tu peux m'envoyer le lien pour moi c est juste les examens d'entrés au BTS.

examen d'entrée pour un BTS services informatiques aux organisations option A : solutions d'infrastructure, systèmes et réseaux

J'essaye d'assimiler les notions de base avant de passer aux choses sérieuses, 25 jours c'est juste!!
A ton avis quelles sont les notions capitales en math pour faire de l'informatique?