Forum de Mathématiques: Maths-Forum

Robot a écrit:Ton erreur, c'est d'écrire quelque chose au hasard qui a vaguement l'air d'un raisonnement alors que tu n'as aucun argument pour le justifier.

Je te donne un contre-exemple : . A-t-on ?

Non,c'est vrai..Je fais quoi alors ?!!

N'écris jamais des trucs au hasard, si tu veux qu'on te prenne au sérieux. D'accord,merci pour le conseil.Sinon,pouvez vous me montrer mes erreurs? et des liens ou des conseils pour que je comprenne mieux? S'il vous plait (je n'ai pas cette leçon dans mon cahier de cours,je suis entrain de ramasser...

Robot a écrit:

Flemme a écrit:

Comment passes-tu de la première ligne à la deuxième ?

Je vais pas vous mentir,je l'ai fait au hasard parce que ça me semblait logique (j'ai donné des chiffres à x et y pour vérifier..)
S'il vous plait,ne soyez pas dur avec moi.

Bonsoir, Pour montrer que E(x+y) = E(x)+E(y)+\epsilon avec \epsilon \in \{0,1\} , on encadre d'abord x par E(x) et y par E(y) . Faîtes cela et ensuite on verra. E(x)\leq x Et E(y)\leq y Donc: E(x)+E(y)\leq x+y Et puisque : x+y\...

Et que : E(x+y)\leq E(y)+E(x) Quel est ton raisonnement pour montrer ça ? Peux-tu donner l'énoncé exact ? Ce signe \prec , c'est pour < ou quoi ? Alors : E(x+y)\leq x+y E(x+y)-x\leq y E(x+y)-x\leq E(y) -x\leq E(y)-E(x+y) E(...

Bonjour,
Bienvenue à toi et toutes mes félicitations pour ton bac!

Bonjouuur, Je souffre toujours avec la partie entière :x ,j'arrive pas à démontrer que : E(x+y)=E(x)+E(y)+\varepsilon ; x,y \in R , \varepsilon \in \left\{0,1 \right\} J'ai montré que : E(x)+E(y)\leq E(x+y) Et que : E(x+y)\leq E(y)+E...

Merci beaucoup. ^^

Razes a écrit:Quel exemple?

Celui là :

Razes a écrit:Soit x=-4.5
Les nombres entiers relatifs inférieurs ou égale à x sont (il y en a une infinité) ..............
La partie entière correspond au plus grand de ces nombre. (fais un essais)

C'est boooon,j'ai compris merciii!!
Et pour l'autre exemple?

C'est le plus grand nombre <=x de plus tu es dans la partie des nombre négatifs. Tu peux tracer un axe avec les nombre entiers relatifs, La partie entière d'un nombre x est son voisin à sa gauche sur l'axe. J'ai pas compris!! Oui,je suis dans la partie des nombres négatifs,on a par exemple -4.5 ,on...

Bonsoir, La partie entière est le plus grand nombre entier relatif n tel que n\leq x , ça veut dire quoi? Pouvez vous me donner des exemples s'il vous plait? On dit le plus "grand nombre" mais on prend le petit?!!! exemple : -2.3 , E(x)= -3 , -3 est plus petit que -2.3 non?!! J'ai vu auss...

Bonsoir, La partie entière est le plus grand nombre entier relatif n tel que n\leq x , ça veut dire quoi? Pouvez vous me donner des exemples s'il vous plait? On dit le plus "grand nombre" mais on prend le petit?!!! exemple : -2.3 , E(x)= -3 , -3 est plus petit que -2.3 non?!! J'ai vu aussi...

Bonjour, Bonsoir, ça fait deux heures que je bloque sur cette question,j'ai tout essayé mais rien..Pouvez-vous m'aider s'il vous plait? Il faut que démontrer que : \alpha = \sqrt[3]{27+6\sqrt{21}} + \sqrt[3]{27-6\sqrt{21}} est un nombre réel naturel. Merci d'avance. il y a plusieurs méthodes pour r...

zygomatique a écrit:salut

on élève au cube et on simplifie/développe/factorise astucieusement ....

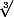
C'est booooon en fait au lieu de travailler avec j'ai calculé (je manque beaucoup de concentration parfois)
Merciii!

Bonsoir,
ça fait deux heures que je bloque sur cette question,j'ai tout essayé mais rien..Pouvez-vous m'aider s'il vous plait?
Il faut que démontrer que :
est un nombre réel naturel.
Merci d'avance.

zygomatique a écrit:salut

plutôt déterminer une limite monotone (qui donne donc le sup ou l'inf suivant la monotonie de la suite)

on peut remarquer que A = 1 - .... ?

C'est bon j'ai compris,merci.^^

Robot a écrit:Vu la tête de l'ensemble A dont les éléments dépendent d'un entier n, quoi de plus naturel que de considérer la suite de ces éléments ?

Pour étudier sa croissance?

Bonsoir! On a : A= \frac{2^n}{2^n -1} ; n\in N* Et il faut déterminer les sup et inf,je les ai trouvé mais quand j'ai vu la correction..ben ils ont utilisé les suites,pourquoi? est-ce que ça marche tout le temps avec les suites? comment? (oui je sais c'est des questions toutes bêtes mais j'ai des pr...

Bonsoir,
Merci à vous,ça me parait plus simple maintenant.

Lostounet a écrit:

Razes a écrit:Soit

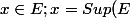Hello Razes,
Comment es-tu certain que le sup est un élément de la partie E?

Cette question m'a poussé à réfléchir,merci!!