Forum de Mathématiques: Maths-Forum

Ok, Je crois avoir trouvé j'ai une limite qui est de : (mais cela me paraît faux)



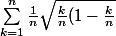J'ai encadrer comme à la question 1 le ln que j'ai obtenu avec la somme et voilà.

Merci encore à toi Ben et aussi à Zygomatique pour la résolution de mon exercice. Je l'ai terminé.

Je continue à développer et ce que je trouverais à la fin me prouvera qu'elle converge , c'est ça ?

Bonjour Ben, Je pense que tu as raison! J'ai inventer le nom je pense car nous ne l'avons jamais nommé clairement dans mon cours. Dans le cours nous avons écrit : On dit que R(f,S) est la somme de Riemann pour f associé à la subdivision pointée S. Cas des subdivisions régulières. n\in N^{*} R(f,...

D'accord, vue avec le produit comme tel je n'y ai pas pensé directement. u_n = \prod_1^n (1 + \dfrac {\sqrt {k(n - k)}}{n^2}) = \prod_1^n (1 + \dfrac 1 n \sqrt {\dfrac k n (1 - \dfrac k n}) Puis ln( \prod_1^n (1 + \dfrac 1 n \sqrt {\dfrac k n (1 - \dfrac k n}&...

Ah d'accord je ne savais pas merci pour l'astuce. C'est la première fois que l'on manipule les suites avec des produits ou des sommes, et je n'ai pas vraiment compris le cours donc je ne me débrouilles pas très bien avec ce type d'exos,

ln(u_n)= ?

D'accord merci Lostounet.
Zygomatique, je ne suis pas sûr de comprendre, je passe alors à :

?


De plus, je n'arrive pas à voir l'intéret de la question (2) pour la question (3) ?

Bonjour,
Je n'avais pas finis d'écrire mon premier message je l'ai modifié j'ai finis la question (2) pour la (1) je vais essayer de faire comme tu l'as dit pour la question (1).

Bonjour, avant tout merci d'avance pour toute éventuelle aide apporté lors de la résolution de mon exercice. J'ai déjà fait les questions 1 et 2 c'es plus pour vérifier, et m'aider à faire la dernière question que je ne comprends pas vraiment. En voici l'énoncé : Pour n\in N^{*} , on pose u_{n}=\pro...

Merci beaucoup pour ton aide Ben, j'ai terminé la question 2, il fallait penser à la petite astuce de réutiliser la question 1). Pour ce qui est de la question 3) Comme on remplace S par Sn je ne sais pas comment commencer je me doute que je vais devoir réutiliser les questions précédentes, mais com...

Merci beaucoup à vous deux! J'ai maintenant réussi à terminer la question (1). Pour la Question (2) j'ai dans mon cours cette définition : Soit f [a,b] -> R. Pour toute subdivision S = ((J_{0},t_{0}),...,(J_{N-1},t_{N-1})) de [a,b], on pose : R(f,S)=\sum_{k=0}^{N-1}{f...

D'accord donc j'obtiens : \int_{u}^{v}{\left|f(t)-f(u) \right|}\leq \int_{u}^{v}{M(t-u)}=[Mt^{2}-Mut] (de u à v) =M\frac{v^{2}}{2}-Muv-(M\frac{u^{2}}{2}-Mu^{2})=M\frac{v^{2}}{2}-Muv=M(\frac{v^{2}}{2}-uv)=M(\frac{v^{2}-2uv}{2}) J'ai du faire une erreur ...

Dur la reprise, comment j'ai pu écrire cette bourde..
Donc oui je venais de revoir dans mon cours le théorème des accroissement finis.
Pour la suite après les accroissements finis, je ne vois pas comment arrivé au résultat, je n'applique pas l'intégrale des deux côtés ?

Bonjour, tout d'abord merci d'avance pour toute éventuelle aide apportée pour la résolution de mon exercice. J'ai donc cet exercice concernant les subdivisions pointées à résoudre. Je bloque pour sa résolution, en voici l'énoncé : Soiti f : [a,b] -> R de classe C1. On pose M=sup\left\{\left|f'&#...

Du fait que f'(a)=f'(b)=0
Par la même méthode que tu as faites Ben, on obtient :



Je ne me trompe pas ?

( :!: Tout comme toi, je suis étudiant en Licence de mathématiques, il faut surtout prendre mon aide comme celle d'un ami qui essaye de faire l'exercice avec toi ; il vaut mieux écouter Ben) Oui je comprends donc tu as bien fait de le faire remarquer :) Je vois où tu veux en venir Ben c'est vrai qu...

Salut Ben,

C'est vrai qu'ici nous sommes dans les complexes donc cela ne marche pas, je galère vraiment avec cette partie du cours ...

Je comprend ta question, il n'y a pas de fonction C2 qui ne sont pas continue, donc f est bien continue...
Mais donc que faire je ne sais d'où partir ?

Exactement! Merci. Pour moi l'inégalité des accroissement finis à cette définition : Soit f une application continue sur un segment [a, b] et dérivable sur ]a, b[. S’il existe M ∈ R tel que f'(x) ≤ M pour tout x ∈]a, b[ alors f(b) − f(a) ≤ M(b − a) (Dans mon cours nous avons fait un exemple avec une...

Bonsoir, je bloque sur mon exercice, et j'aimerais que l'on m'éclaire un peu. En voici l'énoncé: Soit f : [a,b] -> C(complexes) une fonction de classe C^{2} telle que f'(a) = 0 = f'(b) On pose M :=sup \left\{\left|f''(t) \right|; t\in [a,b] \right\} 1)Pour x\in [a,b] , majorer \left|...