12 résultats trouvés
Revenir à la recherche avancée
Re: Événements consécutifs (Proba)
Merci chan pour cette demonstration, même si j'explique mal j'avais pigé le truc et j'ai réussi à faire une bonne rédaction :) Bonjour, Et du coup maintenant il demande de faire varier le nombre de VRAI consécutifs, en faisant quelques calculs j'ai pensé à ça : n est le nombre de tests x est le nomb...
- 25 Jan 2016, 10:38
- Forum: ✯✎ Supérieur
- Sujet: Événements consécutifs (Proba)
- Réponses: 23
- Vues: 1470
Re: Événements consécutifs (Proba)
Bonjour, Et du coup maintenant il demande de faire varier le nombre de VRAI consécutifs, en faisant quelques calculs j'ai pensé à ça : n est le nombre de tests x est le nombre de VRAI consécutifs P_{n,x}=p^2-(p-1)(P_{n-1,x}+pP_{n-2,x}) Avec P_{x,x}=p^x Et P_{x+1,x}=p^x(2-p) V...
- 23 Jan 2016, 15:34
- Forum: ✯✎ Supérieur
- Sujet: Événements consécutifs (Proba)
- Réponses: 23
- Vues: 1470
Re: Événements consécutifs (Proba)
Edit : il aurait mieux valu publier un seul message (on peut modifier un message) plutôt que deux à la suite. Je n'ai vu que le dernier ! Apparemment, tu as compris ce que je te soufflais, mieux que tu ne l'as écrit dans la phrase que je viens de citer. Si une suite ne contient pas deux 1 consécuti...
- 22 Jan 2016, 12:31
- Forum: ✯✎ Supérieur
- Sujet: Événements consécutifs (Proba)
- Réponses: 23
- Vues: 1470
Re: Événements consécutifs (Proba)
Bonjour Robot, as-tu lu mon message précédent ?
Cette formule marche pour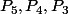 .
.
Xander a écrit:
Cette formule marche pour
- 22 Jan 2016, 10:28
- Forum: ✯✎ Supérieur
- Sujet: Événements consécutifs (Proba)
- Réponses: 23
- Vues: 1470
Re: Événements consécutifs (Proba)
N'as-tu pas vu, je t'ai proposé une méthode : Comment est-ce possible de ne pas avoir deux 1 consécutifs dans une suite de n symboles 0 et de 1 ? Analyser en partant de la fin de la suite, pour avoir une formule de récurrence liant 1-P_n , 1-P_{n-1} et 1-P_{n-2} . Allez, une indication supplémentai...
- 22 Jan 2016, 09:55
- Forum: ✯✎ Supérieur
- Sujet: Événements consécutifs (Proba)
- Réponses: 23
- Vues: 1470
Re: Événements consécutifs (Proba)
Si une suite ne contient pas deux 1 consécutifs et se termine par 0 alors la probabilité que la suite ne contiennent pas deux 1 consécutifs (1-P_n)_0=(1-P_{n-1})*(1-p) Si une suite ne contient pas deux 1 consécutifs et se termine par 1 alors la probabilité que la suite ne con...
- 22 Jan 2016, 09:52
- Forum: ✯✎ Supérieur
- Sujet: Événements consécutifs (Proba)
- Réponses: 23
- Vues: 1470
Re: Événements consécutifs (Proba)
Du coup il faut que je cherche quoi ?
Une résolution de ce système :
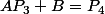
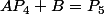
Ou bien une résolution à cette équation :
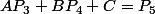
Et encore cela peut être d'autre formes du style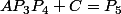
ou alors il existe une autre méthode ? Comment vérifier mon résultat ?
Une résolution de ce système :
Ou bien une résolution à cette équation :
Et encore cela peut être d'autre formes du style
ou alors il existe une autre méthode ? Comment vérifier mon résultat ?
- 20 Jan 2016, 14:40
- Forum: ✯✎ Supérieur
- Sujet: Événements consécutifs (Proba)
- Réponses: 23
- Vues: 1470
Re: Événements consécutifs (Proba)
Juste parce que je viens de faire le calcul,
)
Je vais étudier ce que tu me proposes Robot, je reviendrais sur ce topic si j'ai des questions, merci pour ton aide !
Je vais étudier ce que tu me proposes Robot, je reviendrais sur ce topic si j'ai des questions, merci pour ton aide !
- 19 Jan 2016, 17:34
- Forum: ✯✎ Supérieur
- Sujet: Événements consécutifs (Proba)
- Réponses: 23
- Vues: 1470
Re: Événements consécutifs (Proba)
Il faut que je trouve P en fonction de n . Et effectivement cela ne marche pas pour le cas n=5 car mon calcul donne \frac{20}{32} alors que la vraie proba est de \frac{19}{32} (Si on prend p=\frac{1}{2} ). Et comment trouver cette formule de récurrence ? Et pourquoi est-ce plus facile par 1-P_n ?
- 19 Jan 2016, 17:21
- Forum: ✯✎ Supérieur
- Sujet: Événements consécutifs (Proba)
- Réponses: 23
- Vues: 1470
Re: Événements consécutifs (Proba)
C'est vrai que je n'ai pas pensé l'appliquer,
J'obtiens
)
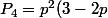)
J'imagine que :
-(n-2)p])
Quelqu'un peut-il me le confirmer ? Car pour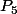 il me reste du
il me reste du 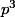 , j'ai du faire une erreur.
, j'ai du faire une erreur.
J'obtiens
J'imagine que :
Quelqu'un peut-il me le confirmer ? Car pour
- 19 Jan 2016, 16:39
- Forum: ✯✎ Supérieur
- Sujet: Événements consécutifs (Proba)
- Réponses: 23
- Vues: 1470
Re: Événements consécutifs (Proba)
Pour n=5 on a :
=4p^2q^3)
=9p^3q^2)
=5qp^4)
=p^5)
On a donc :
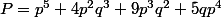
)
On a donc :
- 19 Jan 2016, 15:59
- Forum: ✯✎ Supérieur
- Sujet: Événements consécutifs (Proba)
- Réponses: 23
- Vues: 1470
Événements consécutifs (Proba)
Bonjour, Je suis bloqué sur un problème de proba, je mets les étapes de l'exo : Etape 1 : Un événement se passe 3 fois, la probabilité qu'il soit VRAI vaut p (La probabilité qu'il soit FAUX vaut q). Qu'elle est la probabilité P qu'il soit VRAI 2 fois de suite : p(110)=p(011)=qp^2 p&#...
- 19 Jan 2016, 15:46
- Forum: ✯✎ Supérieur
- Sujet: Événements consécutifs (Proba)
- Réponses: 23
- Vues: 1470
- 12 résultats trouvés - Page 1 sur 1
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
