Forum de Mathématiques: Maths-Forum

Sa Majesté a écrit:Attention : z+i = x+iy+i

Ensuite tu multiplies comme tout à l'heure par la conjugué du dénominateur

(x+iy+i) / i(x+iy)
= ((x+iy+i)(x-iy) / i(x+iy)(x-iy))
= (x²-ixy+ixy-i²y²+ix-i²y) / (ix+i²y)(x-iy)
= (x²+y²+ix+y) / (ix-y)(x-iy)
= (x²+y²+ix+y) / ix²+iy²

Oui et d'ailleurs tu peux vérifier tes réponses au 1 puisque au 2a on te dit "On suppose z distinct de 0, de -i et (1-i)/2" Effectivement, Merci Beaucoup ! Pour la question 2.b , (z+i) / iz ((x+iy) / i(x+iy)) ((x+iy) / (ix+i²y)) (x+iy) / (ix-y)

Sa Majesté a écrit:Petite erreur de calcul ...

Effectivement,

z= (1-i)/2

Oui z=i/(-1+i) Sauf que en général on ne laisse pas un nb complexe sous cette forme (a+ib)/(c+id) Il faut multiplier en haut et en bas par le conjugué du dénominateur (-1-i) pour obtenir un dénominateur réel et non pas complexe Ok , donc z=i/(i-1) = (i(-i-1) / ((i-1)(-i-1))) = (-i²-i) / (-i²-i+i+1)...

Pour la question 2 ,

a/ Pour que les points O , M' et M" soient alignés, il faut que les vecteurs soient colinéaires.
Donc vect OM' = k vect OM"
z+i = k.iz
Et comme k est réel, k=(kiz)/iz

b/ alors là ... je bloque !

Ai-je bon pour le a et comment faire le b ?

Merci

Sa Majesté a écrit:
Il faut faire comme dans IR (factoriser etc ...)
z+i=iz ça donne z(i-1)=i d'où z= ...

z= i/(i-1)

Merci de ton aide . Je planche sur la question 2 et je viens poster pour savoir ton avis.
Merci

[quote="Sa Majesté"]La réponse est bonne mais il te faut 5 lignes pour passer de z+i=0 à z=-i ...


Pour moi , il est logique que z=-i donc je ne vois pas quelle étape il me manque :marteau:

Pour M'=0 z+i=0 a+ib+i=0 a+i(1+b)=0 Il faut que le réel et l'imaginaire soient égals à 0. Donc a=0 et i(1+b)=0 1+b=0 b=-1 Le nombre complexe recherché est z=-i . Pour M'=M'' z+i=iz a+ib+i=+(a+ib) a+i(b+1)=i(a+ib) Mais là je suis bloquée. Merci d'avance pour votre aide

Bonsoir , j'ai 3 exercices sur les nombres complexes. J'en ai déjà fais 2 mais je bloque sur le troisième. Pouvez vous m'aider Svp ? Voilà l'énoncé : Soit M, M' et M'' les points du plan complexe d'affixes respectives : z, z+i et iz. 1/ Pour quel nombre complexe z a-t-on M'=0, origine du repère ? Po...

XENSECP a écrit:Ah merci tu me rassures

Bon on met ça sur le compte de la fatigue

Oui et surtout sur le compte de la maladie .. car faire des maths avec une grippe c'est pas super super .. ^^

Merci encore de m'avoir faire prendre conscience de cette idiotie ^^

A plus tard !

XENSECP a écrit:OMG !



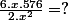
là ça devient inquiétant ^^

Exact , je viens de voir mon erreur et effectivement c'est très très inquiétant !! ^^ Merci !

Personne ne peut m'aider ??

bonsoir, je pense avoir déjà répondu aux 2 premières questions s(x)=2(x*y)+2(2x*x)+2(2x*y) S(x)=2xy+4x²+4xy S(x)=4x²+6xy y=576/2x² S(x)=4x²+6x(576/2x²) S(x)=4x²+1728/x 31/x=>1/12 1728/3=>1728/x=>1728/12 576=>1728/x=>144 36+144<=4x²+1728/x 180<=S(x) Bonjour, merci de ton aide mais il y a un endroit ...

echevaux a écrit:Attention c'est

Oui exacte sur mon brouillon j'ai écrit ça j'ai oublié de le taper sur le pc désolé !

Mais bon ça ne change rien , je suis toujours bloquée à cette endroit ..

UP !!! SVP j'ai besoin de votre aide !

J'ai continué et ça me donne :








:hein:

Pourquoi ne pas mettre tous au même dénominateur dans la deuxième équation. Ca serait dix fois plus simple :zen: Si je mets au même dénominateur la 2eme équation : {R2=20-R1} {1/4.2=(R2/R1R2)+(R1/R1R2)} Je remplace R2 par 20-R1 donc {1/4.2=[(20-R1)/((20-R1)*R1)]+[R1/(20-R1)*R1]} Ai je bon jusqu'ici...

Bonsoir , un exercice de physique dans un livre de maths ... :hum: Pouvez-vous m'aider un peu SVP ?? En courant continu à partir de resistances R1 et R2, on obtient une résistance équivalente a R dans une association en série et une résistance équivalente a r dans une association en dérivation on sa...

ça c'est les solutions en u, il faut maintenant trouver les valeurs de x (tu te souviens qu'on avait dit u=x+1/x) Il faut donc résoudre x+1/x = 2 et x+1/x = 5/2 J'ai résolu ces 2 équations , et j'ai trouvé 3 solutions à (E) . J'ai trouvé pour x+1/x = 2 une solution qui est : x=1 et pour x+1/x = 5/2...

Bonsoir,

J'ai trouvé 3 solutions pour (E) es-ce possible ??