Forum de Mathématiques: Maths-Forum

laetidom a écrit:Ce fut un plaisir ! Bon réveillon !....


Les deux solutions sont :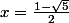

= - 0.618...


= 1.618...(c'est le nombre d'or !)

oui ! merci à vous aussi !

laetidom a écrit:Non 2 !, regarde le graphe, la courbe coupe 2 fois l'axe des abscisses (y=0)

ce qui est égal à 0 c'est l'équation, les 2 solutions sont - 0.618.... et +1.618....

ah oui d'accord j'ai compris ! merci beaucoup de votre aide !

Donc l'équation n'admet qu'une solution : 0 c'est cela ?

laetidom a écrit:je regardes...

super merci !

ensuite, comme je le disait tout àl'heure, il me faut factoriser (x-1/2)²-5/4 sur les conseils de laetidom, j'arrive au résultat suivant : (x-(1+racine5/2))(x-(1-racine5/2)) On me demande, pour conclure ce dm d'en déduire que les solutions dans IR de l'équation x²-x-1=0 qui comprend cette formulatio...

Carpate a écrit:Si
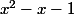
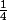
Combien vaut ou autrement dit que faut-il ajouter ou soustraire à pour obtenir ?
Grave question !

x²-x-1 vaut (x-1/2)²-5/4

ok je comprend mieux ! merci

On me demande ensuite de factoriser l'expression (x-1/2)²-5/4 et d'en déduire que les solutions dans IR de l'équation x²-x-1=0

La encore je ne comprend malheureusement pas !

Pouvez-vous m'aider sur ce point la ?

donc dans cette expression , x² = (x-1/2)² ; x =(1/2)² c'est cela ?

Bonjour à tous, j'ai besoin d'aide, on me demande, dans un dm de maths de développer une expression : (x-1/2)². Je la développe grace aux identités remarquables et je trouve x²-x+1/4. On me demande ensuite de déduire que x²-x-1 = (x-1/2)²-5/4 et la je ne sait plus comment faire !!! Ai-je fait une er...

j'ai fait le calcul ainsi : phi^2 + phi et j'ai trouvé le bon resultat !

Ok pour phi au cube et donc pour phi^4, je fait phi^3+phi c'est cela ?

Lostounet a écrit:Salut, est-ce le nombre d'or?

Si oui, on peut remarquer que:
Phi^2=phi + 1
Donc phi^3=phi^2+phi
=2phi + 1

Oui, c'est le nombre d'or

Bonjour,
pour phi = (1+racine5)/2
et non c'est phi au cube et non au carré et phi exposant 4

Bonjour à tous, J'ai besoin de votre aide car, dans un dm que j'ai a rendre pour la rentrée, on me demande de calculer phi au cube puis phi4. J'ai déja essayé de faire les calculs mais la je bloque et je ne trouve pas de vraie solutions. En espérant que quelqu'un pourra m'aider ! Merci d'avance

ok super merci !

Oui c'est en effet la suite de fibonacci ! mais la je ne comprend pas à quoi correspond u ?

Oui c'est cela je n'avait pas trouvé la mise en page ! Merci

non, s'en est une différente. L'équation x² =x+1 j'ai déja eu a la faire avant

Bonjour à tous, je dois faire un dm concernant le nombre d'or et donc le nombre phi qui est égal à (1+racine5)/2 Dans un exercice du dm on me demande de montrer que pour tout entier naturel n, phi est solution de l'équation x n+2 = x n+1 +x n J'espère que quelqu'un sauras m'aider ! merci d'avance !