Forum de Mathématiques: Maths-Forum

Bonsoir
Ta dérivée est fausse je pense. Il faut que tu utilises (fog)'=g' * (f'og)

Ah nan j'ai rien dit, comme x tend vers 0, le 0(x²) aussi et donc on peut l'intégrer au développement de ln et voir qu'on a une limite finie! ^^'

Pour garder le même raisonnement, on peut définir puisque f(0) est non nulle.
Mais j'ai quand même un problème pour déterminer comment tu te débarasse du O(x²) dans le ln

Non, c'est la même chose

Mais si f(0) est différent de 1 ça marche plus :/

Il faut écrire "pour i=1 à n

Lajuuulie a écrit:Je vois vraiment pas...
Je sais pas quoi changer..

Si tu donnes n en entrée de ton algorithme, alors il connaît n.
De plus, dans la boucle de l'algorithme précédent, à la fin de la boucle i on a S=1+2+3+...+i

Donc à quelle valeur de i doit on arrêter la boucle pour avoir 1+2+...+n ?

Lajuuulie a écrit:1) 5 ducoup mdr ?
2) + l'infini ?

1 oui c'est bien 5 :ptdr:
2) non, si tu prends plus l'infini tu vas trop loin. Ici tu donnes un n fixé à ton algo e il calculé la somme jusqu'à n. Avc plus l'infini t'auras "quelques" nombres en trop :lol3:
Indice: dans la première question, n=5

Besoin d'aide pour là questions 1) a) et là questions 2) svp Pour la 1)a, combien de fois executes tu la boucle? Tu le fais pour k=1 puis k=2 puis k=3 puis k=4 puis k=5; donc combien de fois?^^ Pour la 2, dans l'algorithme de l'enonce on fait 1 + 2 + 3 + 4 + 5 . Comment peux-tu faire pour que on co...

mango421 a écrit:Oui pardon on a bien X(0)=2

Qu'entendez vous par forme exponentielle de (1+i)/2 ?

Pour Xn+1 et Yn+1 je tombe sur le bon résultat après développement

bah alors c'est ok
Je parlais du fait que tout complexe peut se mettre sous la forme z=r*exp(i*a) mais tu l'as peut être pas encore vu désolé^^'

De plus le résultat est donné par la suite et semble être Xn+1= (Xn-Yn)/2 et Yn+1=(Xn+Yn)/2 Je ne comprends pas comment on arrive à ce résultat, pourriez-vous m'aider ? Merci d'avance d'avoir pris du temps pour me répondre Si z_n=x_n+iy_n alors z_{n+1}=\frac{1+i}{2}(x_n+iy_n) Tu développes ...

Si je suis ton calcul, le dernier vient de mais ça ça veut dire 50=72 !! :marteau:
Donc là y a une erreur.
Et je pense que tu devrais plutôt regarder le lien entre 72 et 18... :lol3:

Tu calcules l'intégrale en te ramenant à l'intégrale de gauss qui n'est autre que F(a)=\bigint_{-\infty}^{a}{e^{\frac{-x^2}{2}}dx} et que tu peux calculer de plusieurs façon (notamment en utilisant que: \bigint_{x=-\infty}^{a}{\bigint_{y=-\infty}^{a}{e^{\frac{-(x^2+y^2)}{2}}dy}dx}=F&...

Si X non inclus dans A il existe x dans X et pas dans A.
Mais du coup x n'est ni dans A inter X; ni dans B inter C(E)X donc sontradiction avec l'hpothèse de départ qui dit que X est l'union de ces deux ensembles. (on a trouvé un x qui est dans X mais dans aucun des deux autres)

N.L a écrit:C'est quoi comme exos , tu es en quelle filière ?

Ecole d'ingé, actuellement erasmus en allemagne^^
C'est sur les estimateurs de Bayes, je pense pas que t'aies vu encore

Je vais essayer de me débrouiller pour le suivant , si jamais je bloque je te dis ce que j'ai fait et on en parle , merci de ton aide encore une fois ^^ Le suivant est : (A ;) X);)(B ;) C(E) X) = ;) ;);) B ;) X ;) C(E )A Pour le premier déjà, t'as réussi à montrer que si X n'est pas inclus dans A o...

N.L a écrit:Merci P'tipito ^^

Pour me remercier tu peux faire mes exos de stats :lol3:

oui, en gros si tu fais un dessin: une grosse boule pour X, si A inclus dans X tu vois bien que ton A (peu importe sa forme) a sa frontière à l'intérieur de X donc l'intersection des deux est A

biss a écrit:Je viens de remarquer que pourquoi forcément ?
Supposons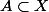
Alors et comme alors
Donc

Si alors plutôt. Là aussi le dessin peut aider

oui
(et comme on peut pas écrire un message de moins de 10 caractère, j'écris autre chose^^')