Forum de Mathématiques: Maths-Forum

C'est un Probleme d'olympiade donc si ça a à voir dans ce forum --'

Bonjour,

Dans un Probleme d'olympiades, qui est le suivant: quatres filles rencontrent quatres garçons. Ils souhaitent former 4 couples garçon-fille de danseurs. Combien de choix ont-ils? La solution est 24, mais je ne comprends pas pourquoi...

Merci d'avance.

Non, désolé ce n'est pas mon compte que je voulais supprimer mais un autre!

C'est la bonne réponse, bravo! :+:

Bonjour,

Comment puis-je supprimer mon compte?
Merci d'avance!

Que veut dire "cst"?

Bonjour,

Pourriez-vous m'aider à prouver que la fonction R:R de l'équation fonctionnelle (pour tous et 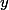est injective? Merci!

Je te conseille d'essayer de résoudre par étapes en notant x=le prix initial des chemises: la première étape est de calculer le prix total des chemises qu'il a vendues au prix initial la deuxième est de calculer le prix total des chemises qu'il a vendues avec la première réduction la troisième est d...

Oui, tu as raison ce n'était pas très clair :lol3: j'ai édité mon message.

Bonjour tout d'abord,

qu'est-ce que tu ne comprends pas? Parce qu'on est là pour t'aider ici, pas pour te donner les réponses... Le problème vient de l'énoncé ou de la résolution?

Bonjour,

Pourriez-vous m'aider à prouver que la fonction R:R de l'équation fonctionnelle (pour tous et 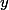) est injective? Merci!

Je pose , etc

Tu sais ce que c'est au moins une inégalité homogène??? Parce que la

Euuuuh, tu le fait exprès?

On a d'abord $((1+a+b+c+d+e))^2\ge4(a^2+b^2+c^2+d^2+e^2)$ avec $0\le a, b, c, d, e\le 1 et a,b,c,d,e réels. L'inéquation n'est pas homogène. On peut ensuite remplacer a,b,c,d,e par $\frac{a}{a'}, ..., \frac{e}{e'}$ . On a donc $(1+\frac{a}{a'}+\frac{b}{b'}...

Utilise x=-y

Réfléchis... Comment pourrais-tu utiliser le fait que f(0)=0? Fais une nouvelle substitution!

Voilà!
Ensuite, tu dois supposer que f(0)=0, qu'est ce que tu peux en déduire de f(x)?

Commence par essayer de trouver combien vaut $f(0)$ avec des substitutions. Je vais t'aider: en substituant x=y=0, tu peut obtenir $f(0+0)=f(0)=f(0).f(0)=f(0)^2$ , donc $f(0)=0$ ou $1$ puisque ce sont les seuls nombres qui sont égaux à leurs ca...

J'imagine que tu veux parler de surjectivité?

Tu sais faire des substitutions? Si oui, commence par faire ça pour t'aider...

Bonjour, j'ai une question à propos des inégalités... Est-ce qu'une équation comme par exemple $(1+\frac{a}{a'}+\frac{b}{b'}+\frac{c}{c'}+\frac{d}{d'}+\frac{e}{e'})^2\ge4(\frac{a^2}{a'^2}+\frac{b^2}{b'^2}+\frac{c^2}{c'^2}+\frac{d^2}{d'^2}+\frac{e^2}{e&...

Oui, en plus, si il était isocèle il serait équilatéral puisqu'il a un angle de 60° :ptdr:

Ok, je comprends ce qu'il faut faire. Je m'y mettrai dans 1 heure ou 2.

Avec quel logiciel as-tu fait ce dessin?