Ok parfait, merci !
En effet, j'ai "pris peur" pour pas grand chose au final, vu qu'après coup, la solution paraît assez évidente !
26 résultats trouvés
Revenir à la recherche avancée
- 10 Fév 2016, 22:27
- Forum: ✯✎ Supérieur
- Sujet: Espérance, variance et covariance.
- Réponses: 4
- Vues: 1219
Re: Espérance, variance et covariance.
Donc si je comprends bien :
 = E(aXf(aX+b)) = \sum_{k=0}^{1}{akf(ak+b)}P([X=k]))
 = \frac{af(a+b)}{2})
Aussi simple soit-il ?
Aussi simple soit-il ?
- 10 Fév 2016, 22:16
- Forum: ✯✎ Supérieur
- Sujet: Espérance, variance et covariance.
- Réponses: 4
- Vues: 1219
Espérance, variance et covariance.
Bonsoir, Je bloque sur une question et j'aurais donc besoin d'un peu d'aide de votre part. Si vous pouviez jeter un coup d'oeil sur ce que j'ai fait (pour voir s'il n'y a pas d'erreur) et m'indiquer le chemin à suivre à l'endroit où je suis bloqué, ce serait super ! L'énoncé nous dit que : X est une...
- 10 Fév 2016, 21:54
- Forum: ✯✎ Supérieur
- Sujet: Espérance, variance et covariance.
- Réponses: 4
- Vues: 1219
- 25 Déc 2015, 21:15
- Forum: ✯✎ Supérieur
- Sujet: Transfert de variables aléatoires.
- Réponses: 2
- Vues: 387
Transfert de variables aléatoires.
J'ai besoin juste d'une petite correction. Soit X une variable aléatoire qui suit une loi exponentielle de paramètre \lambda et Y = {X^3} . On a donc F_{Y} la fonction de répartition Y et F_{X} la fonction de répartition de X qui vaut : F_{X}(x)=\begin{cases} 0 & \text{si }0 < x \\ 1 - e...
- 25 Déc 2015, 11:26
- Forum: ✯✎ Supérieur
- Sujet: Transfert de variables aléatoires.
- Réponses: 2
- Vues: 387
C'est bien le résultat que j'ai trouvé, mais je trouve que ça complexifie les choses de faire un changement de variable. Merci à tous en tout cas ! :++:
- 24 Déc 2015, 18:14
- Annonce globale: [PrépaECE] Bloqué sur une intégrale.
- Réponses: 521
- Vues: 13628
Salut, TU commence par faire une intégration par parties en prenant 4$\ u(x)=x\ et 4$\ v'(x)=-2\lambda xe^{-\lambda x^2}\ ce qui au final t'enlève le 4$x^2 de l'intégrale et il te reste une intégrale de Gauss "classique". Hum ... intéressant. On l'a vu rapidement quand...
- 24 Déc 2015, 00:24
- Forum: ✯✎ Supérieur
- Sujet: [PrépaECE] Bloqué sur une intégrale.
- Réponses: 521
- Vues: 13628
C'est bien ce que j'ai essayé. I = \bigint_{0}^{+\infty} 2 \lambda x^2 (e^{-\lambda x^2}) dx Si je pose u(x)=x et v'(x)=2 \lambda x e^{-\lambda x^2} J'obtiens alors : u'(x)=1 et v(x)=- e^{-\lambda x^2} Et ainsi j'obtiens : I = \left[ -xe^{-\lambda x^2}...
- 24 Déc 2015, 00:06
- Forum: ✯✎ Supérieur
- Sujet: [PrépaECE] Bloqué sur une intégrale.
- Réponses: 521
- Vues: 13628
[PrépaECE] Bloqué sur une intégrale.
Bonsoir, :lol5: Le titre résume assez bien la situation, je suis bloqué sur une intégrale. Rien dans le formulaire des intégrales usuelles ne me permet de débloquer la situation, les intégrations par parties que j'ai tenté ne débouchent sur rien et en ce qui concerne les changements de variable, je ...
- 23 Déc 2015, 23:43
- Forum: ✯✎ Supérieur
- Sujet: [PrépaECE] Bloqué sur une intégrale.
- Réponses: 521
- Vues: 13628
- 21 Aoû 2015, 22:37
- Forum: ✯✎ Supérieur
- Sujet: Fonction intégrale
- Réponses: 3
- Vues: 447
Fonction intégrale
Salut, j'ai une petite question dont la réponse doit être toute bête mais j'aimerais bien comprendre. :spy: Soit la fonction f telle que pour tout x de \mathbb{R^{+}} : f(x) = \frac{2}{x^2} \int_{0\ \ \ }^{\ \ \ x} \frac{t}{e^{t} + 1} dt et f(0)= \frac{1}{2} . En posant h(x) ...
- 21 Aoû 2015, 21:04
- Forum: ✯✎ Supérieur
- Sujet: Fonction intégrale
- Réponses: 3
- Vues: 447
- 14 Aoû 2015, 15:28
- Forum: ✯✎ Supérieur
- Sujet: Problème avec une série
- Réponses: 4
- Vues: 389
- 13 Aoû 2015, 22:19
- Forum: ✯✎ Supérieur
- Sujet: Problème avec une série
- Réponses: 4
- Vues: 389
Problème avec une série
Bonsoir, je bloque sur la série suivante :
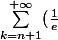^k)
Je sais que, quand , on a :
, on a : 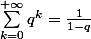 , mais là on ne commence pas à
, mais là on ne commence pas à  donc je ne vois pas.
donc je ne vois pas.
Je compte sur vous pour me débloquer, merci d'avance ! :lol4:
Je sais que, quand
Je compte sur vous pour me débloquer, merci d'avance ! :lol4:
- 13 Aoû 2015, 21:47
- Forum: ✯✎ Supérieur
- Sujet: Problème avec une série
- Réponses: 4
- Vues: 389
Je n'avais pas pensé à vérifier cela, et vérification faite à l'instant, les deux sommes sont bien égales à 1.
Sinon, la première notation que j'ai utilisé était un "sachant que", c'est bien comme cela que ça s'écrit non ?
Sinon, la première notation que j'ai utilisé était un "sachant que", c'est bien comme cela que ça s'écrit non ?
- 11 Aoû 2015, 21:48
- Forum: ✯✎ Supérieur
- Sujet: Exercice espace probabilisé fini
- Réponses: 6
- Vues: 535
Exercice espace probabilisé fini
Salut, j'ai fait un exercice mais je n'ai pas réussi à trouver un corrigé sur Internet. Je fais appel à vous, une fois de plus. :girl2: - Énoncé : On tire, avec remise, cinq boules dune urne contenant dix boules numérotés de 1 à 10 . On note X la var égale au maximum des cinq( * ) numéros obtenus e...
- 11 Aoû 2015, 19:45
- Forum: ✯✎ Supérieur
- Sujet: Exercice espace probabilisé fini
- Réponses: 6
- Vues: 535
Ils somment jusqu'à n-1 pour qu'il ne reste plus que v_n et et v_0 après télescopage. Si tu étais allé jusqu'à n, tu te serais retrouvé avec du v_(n+1). Tu connais les formules pour la somme des k² et pour la somme des k ? Ahhh ok, merci pour ta réflexion. Elle m'a fait réaliser que v_{n}-v_{0} n'é...
- 07 Aoû 2015, 18:05
- Forum: ✯✎ Supérieur
- Sujet: Somme et technique du télescopage
- Réponses: 4
- Vues: 3569
Somme et technique du télescopage
Bonjour, Je n'arrive pas à comprendre le corrigé d'un exercice. Les parties du corrigé que je n'arrive pas à comprendre sont en vert. Énoncé : Soit la suite (u_{n})__{n \in \mathbb{N}} définie par $\left\{ \begin{array}{l} u_{0} = 1 \\ \forall n \in \mathbb{N},\ \ u_{n+1} = 2u_{n}+n(n-1&...
- 07 Aoû 2015, 16:07
- Forum: ✯✎ Supérieur
- Sujet: Somme et technique du télescopage
- Réponses: 4
- Vues: 3569
Merci pour vos réponses. :we: Quelqu'un peut-il me dire si j'ai bon pour la suite ? Pour calculer Im (\phi) : On note \beta = ( E__{1,1} , E__{1,2} , E__{2,1} , E__{1,2} ) base canonique de M_2(\mathbb{R}) . Avec E__{1,1} =\begin{pmatrix} 1 & 0 \\ 0 & 0 \end{pmatrix} ...
- 26 Juil 2015, 00:16
- Forum: ✯✎ Supérieur
- Sujet: Ker d'un espace vectoriel de matrices
- Réponses: 9
- Vues: 749
zygomatique \right Non, ce n'est pas vraiment de la résolution du système dont je doute, c'est du résultat obtenu. Ça voudrait dire que Ker (\phi) = 0__{2,2} Après, peut-être est-ce parce que c'est la première fois que je tombe sur un tel résultat, mais d'habitude je trouve des résultats com...
- 24 Juil 2015, 20:57
- Forum: ✯✎ Supérieur
- Sujet: Ker d'un espace vectoriel de matrices
- Réponses: 9
- Vues: 749
- 26 résultats trouvés - Page 1 sur 2 • 1, 2
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
