Forum de Mathématiques: Maths-Forum

bonsoir, si quelqu'un pourrait m'aider merci d'avance 1. Soit a et b deux entiers relatifs. Démontrer que : (a) Pour tout entier naturel n ;) 1, a^n ;) b^n est un multiple de a ;) b. (b) Si n est un entier naturel impair, alors a^n + b^n est un multiple a + b. (c) Application : Soit a entier relatif...

capitaine nuggets a écrit:De rien, n'hésite pas à revenir au cas où :we:

On pose Tn =t0+t1+...+tn,Wn =w0+w1+...+wn etUn =u0+u1+...+un.

b. Exprimer Tn en fonction de n, puis exprimer Wn en fonction de n.
c. En déduire Un en fonction de n.

capitaine nuggets a écrit:De rien, n'hésite pas à revenir au cas où :we:

j'ai encore une autre question,

on me demande d'exprimer Tn en fonction de n

Tn = t_0 x 1 - ( 1/3 ) ^( n +1) )/ 1 - 1/3 ?

capitaine nuggets a écrit:C'est ce que j'ai dit plus haut, il faut faire apparaître un signe "-" après le "=", en multipliant par "-1".
:+++:

ah d'accord j'ai compris ! merci beaucoup

capitaine nuggets a écrit:Ben oui, et tu obtiens le résultat voulu alors ?

bah je ne vois pas comment obtenir le résultat voulu après parce qu'on veut : tn+1 - T0

Regarde ce que tu as : T_n= \frac 3 2 t_0 \times \left( 1 - \left( \frac 1 3 \right)^{n+1} \right) Regarde ce que tu veux avoir T_n = - \frac 3 2 ( t_{n+1} - t_0) . Déjà, dans le résultat qu'on veut, il y a un symbole " - " après le symbole " = " donc il ...

Relis ce que tu as écrit, l'expression de T_n contient le facteur t_0 = \frac{19} 4 qu'il te manque pour faire apparaître t_{n+1} : [CENTER] T_n= \frac 3 2 t_0 \times \left( 1 - \left( \frac 1 3 \right)^{n+1} \right) [/CENTER] :+++: Tu peux au passage changer de signe, à la fin on v...

capitaine nuggets a écrit:Oui, mais il est contenu dans l'expression de , que vaut ?

comment ça contenue dans l'expression de Tn ?

t_0 = 19/4

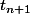
capitaine nuggets a écrit:Exprime-moi , et regarde ce qu'il manque dans l'expression de pour faire apparaître .

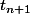
t_n+1 = 19/4 x ( 1/3 )^(n+1)

il manque donc 19/4

capitaine nuggets a écrit:Essaye de mettre des parenthèse pour qu'on comprenne bien l'ordre des opération, sinon ça sème le doute :++:

Voilà, c'est quasiment fini, regarde ce que tu veux obtenir et tu tomberas sur ce que tu veux :+++:

mais je ne vois pas comment faire apparaître le t_n+1

chan79 a écrit:Pour la question e, OK pour afficher (a+b)/2 (valeur approchée à 1/1000)
Pour la question f, si on remplace 0.001 par 0.0001 (soit Tant que b-a>0.0001), la valeur affichée sera une valeur approchée au 1/10000

d'accord merci

L'idée c'est de transformer le quotient \frac{ 1 - \left( \frac 1 3 \right)^{n+1} }{ 1 - \frac 1 3 } en produit (entre parenthèses, tu peux remarquer que tu as un début d'expression de t_{n+1} avec le \left( \frac 1 3 \right)^{n+1} au numérateur :++: ) j'obtient donc : 3/2 x to x 1 ...

Landstockman a écrit:C'est quel modèle ? (Simple curiosité hein)

ti nspire cx cas

Landstockman a écrit:Non ce n'est pas la peine mais quand on te demande les valeurs donne les valeurs approchées...
Ta machine te donne toujours des valeurs exactes ?

oui pratiquement

capitaine nuggets a écrit:Tu y es presque, réduit au même dénominateur et met-le en facteur avec :++:

j'obtient donc 2/3, mais je ne vois pas comment le mettre en facteur :mur:

Salut ! Je pense qu'il y a une erreur dans ton énoncé : je pense plutôt que u_0=1 , sinon à la fin, on obtient pas la bonne expression de t_n ... D'après l'énoncé v_n = 4 u_n - 6n + 15 donc u_n=... . Maintenant, regarde ce que tu veux obtenir et reconnait le terme w_n= \frac 3 2 n - \frac{15}{ 4} d...

Carlalprs a écrit:donc approx (a+b)/2 en sortie?

j'obtient donc directement 1,48975 arrondi au millième près c'est ça?

Landstockman a écrit:Pas besoin de l'écrire dans l'algorithme mais pour donner les valeurs arrondis

donc approx (a+b)/2 en sortie?

Landstockman a écrit:D'accord :we:
Mais peut être qu'il vaut mieux afficher une valeur décimale...

je peux pas mettre approx dans mon algo pour avoir une valeur décimale?

Landstockman a écrit:Oui c'est vrai...
Du coup ta ligne c'est :
Afficher ?

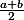
oui exacte et j'obtient : 3051/2048 au millième près