179 résultats trouvés
Revenir à la recherche avancée
Bonjour
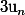
est une suite définie pour tout entier naturel n non nul par
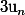
=
dt)
merci pour ton aide (c'était la partie B du problème, je n'ai mis que la partie C)
Cordialement
- par lexot
- 07 Avr 2007, 18:09
-
- Forum: ✎✎ Lycée
- Sujet: Suite définie par une intégrale
- Réponses: 2
- Vues: 936
Bonjour J'ai un exo en 3 parties. Seule la question 3 me pose des difficultés. Merci de m'apporter votre aide : http://carremaths2.yellis.net/fichier/06040724Suite_Integ12.jpg Voici ce que j'ai rédigé : http://carremaths2.yellis.net/fichier/06040726Suite_integ3.jpg Cordialement
- par lexot
- 07 Avr 2007, 11:42
-
- Forum: ✎✎ Lycée
- Sujet: Suite définie par une intégrale
- Réponses: 2
- Vues: 936
Bonsoir Si une fonction f est dérivable en un point x0, alors elle est continue en x0. Par contre l'inverse est faux : Si une fonction f est continue en un point x0, alors elle n'est pas forcément dérivable en x0 . Ex : 3$\sqrt{x} est continue au point 0, mais n'est pas dérivable en 0. Cordialement
- par lexot
- 17 Mar 2007, 22:44
-
- Forum: ✎✎ Lycée
- Sujet: derivabilité
- Réponses: 2
- Vues: 471
Bonjour cos(a+b)=cos a * cos b - sin a * sin b (1) et sin(a+b)=sin a * cos b + sin b * cos a (2) cos(a-b)=cos a * cos b + sin a * sin b (3) sin(a-b)=sin a * cos b - sin b *cos a (4) (1)+ (3) => 2cos a * cos b = [cos(a+b) + cos(a-b)] (3) -(1) => 2sin a * sin b = [cos(a-b) - cos(a+b)] on déduit que: c...
- par lexot
- 17 Mar 2007, 21:48
-
- Forum: ✎✎ Lycée
- Sujet: aide en maths svp!
- Réponses: 1
- Vues: 495
Bonjour
1) 2sinx = 0 => x = K
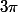
avec K dans Z
Revoie ton énoncé, car les points O, A, et B ne sont pas alignés (erreur dans les coordonnées?)
O, A, et B sont alignés si les vecteurs OA et OB sont colinéaires
si B[2 ; (3pi)/4], O, A, et B sont alignés(est-ce là l'erreur?)
Cordialement
- par lexot
- 09 Mar 2007, 16:36
-
- Forum: ✎✎ Lycée
- Sujet: 2 ou 3 question sur les angles orientés...
- Réponses: 4
- Vues: 590
Bonjour D est le barycentre de (B;1),(C;1)et(E;-1), donc : \vec{DB} + \vec{DC} - \vec{DE} = \vec{0} démontrable en géométrie de 2nde D est le barycentre de (B;1),(C;1)et(E;-1), donc : \vec{FB} + \vec{FC} - \vec{FE} = \vec{FD} (1) F milieu de A et D, donc F est le barycentre de (A;1), et(D;1), donc :...
- par lexot
- 25 Fév 2007, 06:49
-
- Forum: ✎✎ Lycée
- Sujet: Barycentre 1ere S
- Réponses: 5
- Vues: 568
Bonjour J'ai un DM sur les calculs analytiques en geometrie de l'espace Voici l énoncé Soit ABCDEFGH un cube d'arete =a , I le centre du carré EFGH et J le centre du carré BCGF 1) En se placant dans un repere orthonormal D,DA,DC,DH déerminer les coordonées des points A,I et J je pense avoir trouvé ...
- par lexot
- 23 Fév 2007, 23:41
-
- Forum: ✎✎ Lycée
- Sujet: DM calcul vectorielle
- Réponses: 3
- Vues: 1970
Bonjour
Pour calculer l'angle pour un cos de 0.8, on utilise la formule
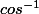
(0.8) avec une calculatrice. Sinon, tu traces un triangle rectangle ABC rectangle en A, avec AC = 8cm et BC=10cm, et tu mesures la valeur de l'angle C.
Pourquoi veux-tu connaitre l'angle sans calculatrice?
Cordialement
- par lexot
- 22 Fév 2007, 14:20
-
- Forum: ✎✎ Lycée
- Sujet: Calculer un angle a partir de son cosinus sans calculatrice
- Réponses: 11
- Vues: 57949
Bonjour Avec une table, on sait la valeur du cosinus de tous les angles remarquables : de 0, 30°, 45°, 60°, 90° cos(0°) = 1 ; cos(60°) = 0.5 ....etc Soit un triangle ABC rectangle en A ; cos(C) = \frac{AC}{BC} ; c'est la seule formule qui permet d'avoir le cosinus d'un angle (niveau lycée) sans calc...
- par lexot
- 22 Fév 2007, 13:44
-
- Forum: ✎✎ Lycée
- Sujet: Calculer un angle a partir de son cosinus sans calculatrice
- Réponses: 11
- Vues: 57949
Bonjour
Connais-tu le théorème de Thalès?
0

x

11
Courage pour la suite
Cordialement
- par lexot
- 22 Fév 2007, 12:54
-
- Forum: ✎✎ Lycée
- Sujet: Le verre à cocktail
- Réponses: 11
- Vues: 1492
Bonjour
Connais-tu le théorème de Thalès?
0 <= x <= 11
Courage pour la suite
Cordialement
- par lexot
- 22 Fév 2007, 12:17
-
- Forum: ✎✎ Lycée
- Sujet: Le verre à cocktail
- Réponses: 11
- Vues: 1492
Bonjour 3$u_n = 3$u_0 + n.r 3$u_2 = 3$u_0 + 2.r 3$u_7 = 3$u_0 + 7.r 3$u_{10} = 3$u_0 + 10.r 3$u_2 + 3$u_7 = 2 3$u_0 + 9.r on obtient le système suivant 2 3$u_0 + 9.r = 9 3$sqrt{2} + 2 3$u_0 + 10.r = 10 3$sqrt{2} + 1 2 3$u_0 + 20.r = 20 3$sqrt{2} + 2 -2 3$u_0 - 9.r = -9 3$sqrt{2} - 2 11.r = 11 3$sqrt...
- par lexot
- 22 Fév 2007, 04:17
-
- Forum: ✎✎ Lycée
- Sujet: Exercices sur les suites arithmètiques
- Réponses: 3
- Vues: 1117
Bonjour F milieu de [ED] => F est le barycentre des points pondérés {(E,-2);(D,-2)}, par associativité F est le barycentre des points pondérés {(A,-1);(B,2);(C,-3);(D,-2)}, donc : - \vec{FA} +2 \vec{FB} -3 \vec{FC} -2 \vec{FD} = \vec{0} (1) G= Bar {(A,1);(D,2)} => \vec{FA} +2 \vec{FD} =3 \vec{FG} H=...
- par lexot
- 21 Fév 2007, 22:36
-
- Forum: ✎✎ Lycée
- Sujet: tétraèdre et barycentres
- Réponses: 4
- Vues: 803

