Forum de Mathématiques: Maths-Forum

Merci à vous :)

Il y a et donc les lignes de niveau sont en polaires !

D'accord merci

Mais je dois simplifier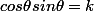 pour se ramener à l'equation de quelque chose que l'on reconnait mieux ?

J'ai mais je ne vois pas comment m'en servir !

Si j'essaie de trouver les lignes de niveau de j'aurai les lignes de niveau de et non de f(x,y) !

Bonjour à tous :) Je bloque sur cet exercice : Soit f(x,y) = \frac{xy}{x^2+y^2} . Calculer g (r,\theta)=f(r cos \theta, r sin \theta) En déduire les lignes de niveau de f. J'ai bien trouvé g (r,\theta) mais je ne vois pas comment m'en servir pour trouver les lignes de niveau ...