Forum de Mathématiques: Maths-Forum

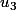
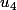
chan79 a écrit:On voit bien qu'une combinaison linéaire de et a comme projeté un vecteur colinéaire à (2,3,3,2).

Merci de ton aide Chan, je pense que j'en suis venu à bout!!!!

chan79 a écrit:Salut
OK pour ta matrice à la question 1.
En l'utilisant, tu peux montrer que

Ok merci, mais comment calcule t'on les images demandées?

Bonjour à tous. Voici l'exercie que je cherche à résoudre: Soit E=\mathbb{R^4} muni de sa structure euclidienne canonique. On pose u_1=(1,2,1,1) ~u_2=(1,1,2,1) ~u_3=(1,1,1,2) ~et ~u_4=(2,1,1,1) H=[u_1,u_2] , F=[u_3,u_4] , et G l'hyperplan d'équation cartésienne x+2y-z...

mathelot a écrit:p(x)=x équivaut à

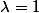
donc est valeur propre, le sous espace propre est de dimension dim(E)-1
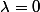
est valeur propre, le sous espace propre est de dimension 1

Merci de ton aide.

Bonjour, Je me retrouve face à un problème simple en apparence, mais... Soit u un vecteur unitaire de (E,N) euclidien. On pose P: E \rightarrow E tel que p(x) = x - \phi(x,u)u . Il faut montrer que p est une projection orthogonale et trouver ses valeurs propres. J'ai essayé de calcul...

Bonjour à tous, J'ai un problème avec une série de fonction: f_n=\frac{cos(nx)}{1+n^2x^2} , x\in\mathbb{R} Déjà f_n paires donc on effectue l'étude sur \mathbb{R^+} J'ai prouvé la convergence simple, en effet \frac{|cos(nx)|}{1+n^2x^2} \leq\frac{1}{n^2x^2} qui est le terme général d'...

mathelot a écrit:Les sont des couronnes

Donc entre la boule de centre 0 et de rayon n et ???

Bonjour voici mon problème: J'ai un compact K_n:=\{x\in\mathbb{\bar B}(0,n)\ :\ \delta_\Omega(x)\geq \frac{1}{n}\} Nous travaillons avec la norme euclidienne sur \mathbb{R^2} et \delta_\Omega(x) = \inf_{y\in \mathbb{R^2}-\Omega} \left\|x-y\right\| Mon ensemble \Omega:=\{(...

Salut, si on veut une démo rapide avec la norme classique, je me suis dit : Je me place avec les complexes. Prenons un cercle de rayon R et un autre de rayon r, strictement positifs, centrés en O. Soit x et x' deux points respectivement sur ces cercles. On a donc : d(x,x') = |Re^{i\thet...

mounch1810 a écrit:Ok, merci beaucoup pour ces précisions

Bon, je nage et je ne parviens pas à démontrer

ça ne change strictement rien !!!! puisque et surtout que les ensembles sont définis par des inégalités !!!! et que l'inf vérifie qu'il est (le) plus petit que tous !! et par définition d(x, A) = h => il existe y dans A (ou son adhérence) tel que d(x, y) = h il n'y a aucun calcul à effectuer ... pa...

salut je sais pas mais tout simplement : si x vérifie d(x, A) =< 2 alors ça signifie simplement qu'il existe un point a de A tel que d(x, a) =< 2 et on sait que d(x, a) = d(a, x) ... donc la solution est triviale .... donc on prend une pièce de 2 € on place son centre sur le cercle A et on fait gli...

Trop fort, merci beaucoup!!!

wow, jolie!!!

Il s'agit de la norme euclidienne.
Par contre, comment écrire les calculs?
???

BiancoAngelo a écrit:Il n'y a pas une définition explicite à "ta" distance d'un point à une partie ?

Si pardon,

Bonjour, Nous sommes dans \mathbb{R^2} . A est un cercle de centre 0 et de rayon 1. Je cherche à déterminer les ensembles suivants: \Lambda_0 := \{x\in \mathbb{R^2} \: d(x,A)\leq 2\} \Lambda_1 := \{x\in \mathbb{R^2} \: d(x,A)<\frac{1}{2}\} Je dois également trouver l'intérieur et la ...

zygomatique a écrit:non i ne contient que des réels de l'intervalle [0, 1] ...

mais I contient-il 0 ? 1 ?

il faut que u = a + t(b - a) appartienne au complémentaire de Oméga ...

Je pense que I mais 1 non

salut c'est plutôt I = \{ t \in [0, 1] \ a + t(b - a) \in \mathbb{R}^n - \Omega \} et alors que se passe-t-il pour t = 0 ? t = 1 ? si \Omega est ouvert alors son complémentaire est fermé ... Oui effectivement I a la forme que tu as mentionnée. Par contre je ne comprends pas le sens de ta qu...

Bonjour à tous, J'ai vraiment des carences en topo, si vous pouviez m'aider sur cet exercice: Soit n \geq 1 et soit \Omega un ouvert non vide de \mathbb{R}^n tel que \Omega soit strictement contenu dans \mathbb{R}^n . On pose: \delta_\Omega(x):=\inf_{y\epsilon\mathbb{R}^n-\Omeg} || x-y|| , x...