Forum de Mathématiques: Maths-Forum

merci quand même

Bonjour tout le monde
J'ai une petite question à vous poser: si on a , peut-on dire directement que ?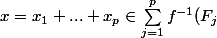
Merci.

je suis vraiment bête, merci, merci beaucoup.

Merci d'avoir répondu, et le dénominateur, comment ~ ?

Bonjour Je dois résoudre cet exercice: Soit (u_n) n;)0 la suite définie par u_0 ;)[0,1] et ;)n;)N, u_{n+1}=u_n - u_n^2 a) Quelle est la nature de la série de terme général u_n ? b) Même question lorsque u_n est définie par la récurrence u_{n+1}=u_n-u_n^{1+\alpha} (avec \alpha>0) . Je...

Je n'arrive même pas à comprendre la solution proposée: Sachant Sachant E_{i,j}E_{k,;)}=;)_{j,k}E_{i,;)}, UE_{i,j} = \sum_{k=1}^n u_{k,i}E_{k,j} Dans la base ((E_{1,1},…,E_{n,1}),(E_{1,2},…,E_{n,2}),…,(E_{1,n},…,E_{n,n})), la matrice de ;) est diagonale par blocs avec des blocs diagonaux chacun égau...

Bonjour :) On considère un R-espace vectoriel de dimension finie E, u un endomorphisme de E, U=(u_{i,j}) la matrice de u dans une base de E, e_{i,j} les projecteurs associés à cette base et E_{i,j} la matrice de ces projecteurs. On considère ;) l'endomorphisme dans L(E) tel que ;)(v)=u;)v a) Montrer...

@ Zaidoun, je crois que vous avez raison car je retrouve le même résultat ((- ;)) n'est pas une valeur propre de A), y aurait-il alors une faute dans le corrigé?

@Zaidoun, det(A + I_{3}) 0 ssi (- ) n'est pas une valeur propre de A, je ne comprends pas cette partie de votre réponse et cela contredit ce que j'ai trouvé dans le corrigé.
@Manny06, non aucune.

Merci

Bonjour tout le monde je suis en train de faire cet exercice mais je n'arrive pas à répondre à la troisième question et je ne comprends pas la réponse proposée par le corrigé, voilà l'énoncé: Soit la matrice A= 0 -b a b 0 -c -a c 0 a) A est-elle diagonalisable dans M_3( \mathbb{R} ) ? b) A est-elle ...