83 résultats trouvés
Revenir à la recherche avancée
Martingale stricte
Bonjour à tous, J'ai à ma disposition les données suivantes: M_t = \frac{1}{||x_0 + W_t||} où ||.|| est la nome euclidienne, x_o \in R_* et W_t mouvement brownien dans R^3 . J'ai déjà du prouver que M_t = - M_t ^2 \part B_t où B_t est un mouvement brownien (je ne sais pas si ce point peut aider sur ...
- 11 Mar 2010, 15:37
- Forum: ✯✎ Supérieur
- Sujet: Martingale stricte
- Réponses: 0
- Vues: 833
Merci beaucoup pour votre réponse.
Si l'on stoppe le mouvement brownien à 0, dans ce cas la martingale n'est plus strictement positive, il faudrait le stoppé pour un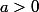 ... Mais j'ai compris l'idée (je chipote juste un peu ^^), merci beaucoup encore une fois.
... Mais j'ai compris l'idée (je chipote juste un peu ^^), merci beaucoup encore une fois.
Cdlt,
Si l'on stoppe le mouvement brownien à 0, dans ce cas la martingale n'est plus strictement positive, il faudrait le stoppé pour un
Cdlt,
- 18 Jan 2010, 13:14
- Forum: ✯✎ Supérieur
- Sujet: Martingale strictement positive ?
- Réponses: 2
- Vues: 960
Martingale strictement positive ?
Bonjour à tous, Une petite question sur laquelle j'ai peur de manqué quelquechose, dans un quizz il est demandé : "Est-il possible qu'une martingale à temps continu soit toujours strictement positive ?" Je pense que oui, en justifiant par une martingale presque surement constante avec une valeur str...
- 18 Jan 2010, 10:45
- Forum: ✯✎ Supérieur
- Sujet: Martingale strictement positive ?
- Réponses: 2
- Vues: 960
Pb pour montrer la positivité de 2 fonctions
Bonjour, Dans un problème je tombe sur cette question : Soit f et g deux fonctions de \mathbb{R} dans \mathbb{R} tel que : \frac{df}{dt}(t)=f(t)(1-g(t)) et \frac{dg}{dt}(t)=g(t)(f(t)-1) . Je dois montrer que si f(0) et g(0&#...
- 17 Avr 2009, 15:09
- Forum: ✯✎ Supérieur
- Sujet: Pb pour montrer la positivité de 2 fonctions
- Réponses: 1
- Vues: 750
Bonsoir, Je viens avec un nouveau problème de calcul de résidu, concernant cette fois \frac{z}{ch(z)} J'ai trouvé que les pôles étaient de la forme z = \frac{i\pi}{2} + 2ik\pi avec k entier relatif... Mais je n'arrive pas à aboutir avec un DL pour le calcul du résidu, je m'y prend peut être ...
- 15 Nov 2008, 18:56
- Forum: ✯✎ Supérieur
- Sujet: Calcul de résidus
- Réponses: 5
- Vues: 1289
Merci beaucoup yos pour ta réponse, je ne pensais plus du tout au DL... Je vais voir si ça fonctionne avec toutes les autres fonctions que j'ai à faire :-)
Bonne journée !
Bonne journée !
- 15 Nov 2008, 12:18
- Forum: ✯✎ Supérieur
- Sujet: Calcul de résidus
- Réponses: 5
- Vues: 1289
Merci.entier plutôt.
Citation: Posté par pluto74 (tous d'ordre 1). Qu'est-ce qui te fait dire ça?
En effet la encore je suis allé un peu vite... ils sont plutôt d'ordre 2... merci.
J'avoue que je ne vois toujours comment avancer sinon ! :briques:
- 15 Nov 2008, 11:11
- Forum: ✯✎ Supérieur
- Sujet: Calcul de résidus
- Réponses: 5
- Vues: 1289
Calcul de résidus
Bonjour, Je dois déterminer les pôles (et leur ordre de multiplicité) puis calculer les résidus correspondants pour : \frac{1}{cos(z) + 1} pour les pôles c'est évident ils sont de la forme : z= \Pi + 2k\Pi avec k entier relatif (tous d'ordre 2). par contre je ne me souviens plus comment l'on...
- 15 Nov 2008, 10:16
- Forum: ✯✎ Supérieur
- Sujet: Calcul de résidus
- Réponses: 5
- Vues: 1289
- 08 Nov 2008, 12:34
- Forum: ✯✎ Supérieur
- Sujet: décomposition en éléments simples
- Réponses: 6
- Vues: 861
ahhhhhhhhhhhhhhhhhhh !!!!
bon je verrais ça plus tard alors !! mais merci pour ta non-confirmation du résultat !! :cry: :king:
bon je verrais ça plus tard alors !! mais merci pour ta non-confirmation du résultat !! :cry: :king:
- 08 Nov 2008, 12:13
- Forum: ✯✎ Supérieur
- Sujet: décomposition en éléments simples
- Réponses: 6
- Vues: 861
- 08 Nov 2008, 11:54
- Forum: ✯✎ Supérieur
- Sujet: décomposition en éléments simples
- Réponses: 6
- Vues: 861
décomposition en éléments simples
Bonjour, je bloque depuis 30min sur la décomposition en éléments simples de cette fonction ! (Le but étant de la transformer en série de Laurent après...) \frac{z+2}{(1-z)((4+3i)-z)} Si quelqu'un pouvait apporter un regard frais la dessus ce serait sympa ! D'avance merci !
- 08 Nov 2008, 11:34
- Forum: ✯✎ Supérieur
- Sujet: décomposition en éléments simples
- Réponses: 6
- Vues: 861
Si a,b,c sont 3 termes consécutifs, alors on a par exemple 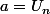 ,
, 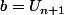 et
et 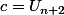 ;
;
Les termes d'une suite arithmétique sont de la forme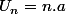 et ceux d'une suite géométrique
et ceux d'une suite géométrique 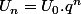 ...
...
Les termes d'une suite arithmétique sont de la forme
- 13 Juil 2008, 14:46
- Forum: ✎✎ Lycée
- Sujet: problèmes sur les suites
- Réponses: 5
- Vues: 1089
Dérivée d'une forme différentielle ???
Bonjour,
Dans un exercice je rencontre la question suivante :
On pose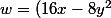 .dx - 8 xy .dy) . Calculer
. Calculer 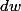 .
.
La réponse prend certainement une ligne mais je ne sais plus comment il faut faire... Comment dérivée-t-on une forme différentielle ? :marteau:
D'avance merci !
Dans un exercice je rencontre la question suivante :
On pose
La réponse prend certainement une ligne mais je ne sais plus comment il faut faire... Comment dérivée-t-on une forme différentielle ? :marteau:
D'avance merci !
- 29 Mai 2008, 09:42
- Forum: ✯✎ Supérieur
- Sujet: Dérivée d'une forme différentielle ???
- Réponses: 1
- Vues: 1054
- 19 Mai 2008, 15:51
- Forum: ✯✎ Supérieur
- Sujet: inégalité à montrer
- Réponses: 8
- Vues: 956
- 19 Mai 2008, 13:09
- Forum: ✯✎ Supérieur
- Sujet: inégalité à montrer
- Réponses: 8
- Vues: 956
- 19 Mai 2008, 12:44
- Forum: ✯✎ Supérieur
- Sujet: inégalité à montrer
- Réponses: 8
- Vues: 956
inégalité à montrer
Bonjour, Voici mon soucis : Montrer que \forall t \in [0, \Pi ] : sin(t) \ge t - \frac{t^3}{3!} + \frac{t^5}{5!} - \frac{t^7}{7!} (On pourra partir de linégalité cos(t) \le 1 , montrer que sin(t) \le t puis que cos(t) \ge 1 - \frac{t^2}{2} , etc.. Rédiger la démonstr...
- 19 Mai 2008, 12:29
- Forum: ✯✎ Supérieur
- Sujet: inégalité à montrer
- Réponses: 8
- Vues: 956
- 18 Mai 2008, 12:46
- Forum: ✯✎ Supérieur
- Sujet: Question de Cours => Rotation dans R^3
- Réponses: 1
- Vues: 737
Question de Cours => Rotation dans R^3
Bonjour, J'ai un trou de mémoire avec la chose suivante : Soit A une isométrie positive de \mathbb{R}^3 A = \frac{1}{3} \begin{pmatrix} -2&-1&2 \\ 2&-2&1 \\ 1&2&2 \end{pmatrix} On a donc Tr( A ) = 1 + 2.cos( \alpha ) soit cos( \alpha ) = \frac{-5}{6} m...
- 18 Mai 2008, 08:36
- Forum: ✯✎ Supérieur
- Sujet: Question de Cours => Rotation dans R^3
- Réponses: 1
- Vues: 737
- 83 résultats trouvés - Page 1 sur 5 • 1, 2, 3, 4, 5
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
