42 résultats trouvés
Revenir à la recherche avancée
Re: réduction d'un grand nombre à 1 ou 0
Bonsoir, Ton algorithme réduit tout le monde à 0. Il y a un moyen très rapide de faire ça : retourner 0 quelle que soit l'entrée. D'où la demande de si on pouvait le faire par étapes avec les contraintes annoncées. Il y a plein d'algorithmes qui existent mais recourent à la vérification de parité, ...
- 14 Aoû 2022, 14:23
- Forum: ✯✎ Supérieur
- Sujet: réduction d'un grand nombre à 1 ou 0
- Réponses: 3
- Vues: 260
réduction d'un grand nombre à 1 ou 0
Bonjour, On peut réduire n'importe quel entier naturel rapidement à 1 ou 0 simplement avec cet algorithme : si x est pair alors x=x/2 si x est impair alors x=x-1 Mais existe-t-il un algorithme rapide pour faire une réduction similaire par étapes, en ayant les contraintes suivantes : - sans vérifier ...
- 13 Aoû 2022, 21:39
- Forum: ✯✎ Supérieur
- Sujet: réduction d'un grand nombre à 1 ou 0
- Réponses: 3
- Vues: 260
Re: bornes des coefficients d'une surface polynomiale
tu ne cherches pas la solution passant par tous les points car elle n'existe pas dans le cas général, mais une solution optimale selon une norme donnée. Il y a une optimisation matricielle par la méthode des moindres carrés qui est pour un pol de degré 4, un système 5*5. cf "optimisation systè...
- 28 Avr 2019, 09:44
- Forum: ✯✎ Supérieur
- Sujet: bornes des coefficients d'une surface polynomiale
- Réponses: 3
- Vues: 440
bornes des coefficients d'une surface polynomiale
Bonjour, J'ai un nuage de points (xi,yi,zi) auxquels je voudrais ajuster un polynôme d'ordre 4. Analytiquement, cela revient à trouver les 15 coefficients du polynôme en résolvant le système linéaire A*[X]=[Z] , donc à inverser la matrice A qui sera carrée en sélectionnant 15 points. Problème 1 : Co...
- 27 Avr 2019, 21:54
- Forum: ✯✎ Supérieur
- Sujet: bornes des coefficients d'une surface polynomiale
- Réponses: 3
- Vues: 440
Re: déterminer la fonction d'une pente
Pour ce que tu veux faire, des courbes polynomiales suffisent. Plus précisément comme ça a été dit avant: une courbe symétrique définit par F(x)=ax²+bx+c va très bien fitter tes trois points. Si ça ne marche pas, c'est qu'une question de programmation! Essaye d'abord de faire ce que tu veux à plat p...
- 05 Mai 2017, 07:50
- Forum: ⚜ Salon Mathématique
- Sujet: déterminer la fonction d'une pente
- Réponses: 9
- Vues: 753
notation ensemble de bi-points
bonjour,
considérant n bi-points de réels (x,y), l'ensemble qui les décrit est noté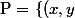 \in {R^{{2^n}}}} \right\}$) ou bien
ou bien 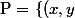 \in {R^{{n^2}}}} \right\}$) ?
?
considérant n bi-points de réels (x,y), l'ensemble qui les décrit est noté
- 04 Mai 2017, 15:22
- Forum: ✎✎ Lycée
- Sujet: notation ensemble de bi-points
- Réponses: 1
- Vues: 230
Re: Rotation dans R3
- Comme tu connais deux vecteurs, le produit vectoriel te donnera le 3ème vecteur. Ainsi tu obtiens la base associée à ton objet qui bouge après avoir tout normalisé. - Avec les coordonnées des vecteurs de la base créée tu remplie ta matrice de passage "appelée P" de la base fixe à la base...
- 15 Fév 2017, 12:14
- Forum: ✯✎ Supérieur
- Sujet: Rotation dans R3
- Réponses: 8
- Vues: 730
systeme equations differentielles
Bonjour, J'ai le système suivant avec les fonction \[e:R \to R\] et \[h:R \to R\] ( k1 et k2 des constantes dans R ): \left\{ {\begin{array}{*{20}{c}} {\frac{{{\partial ^2}e(t)}}{{\partial {t^2}}} = {k_1}\sqrt {{{\left( {\frac{{de}}{{dt}}} \right)}^2} + {{\left( {\frac{{dh}}{{dt}...
- 15 Déc 2016, 16:42
- Forum: ✯✎ Supérieur
- Sujet: systeme equations differentielles
- Réponses: 1
- Vues: 241
Re: Recherche formule analytique
- 07 Déc 2016, 16:07
- Forum: ⚜ Salon Mathématique
- Sujet: Recherche formule analytique
- Réponses: 3
- Vues: 525
Re: appliquer newton-raphson
juste pour info car j'ai déjà résolu mon problème: le nom complet de l'algo c'est : "downhill simplex method" appelé aussi "Nelder–Mead method" qui marche pour de l'optimisation non linéaire sans contraintes. Dans mon problème je sais que min(f(x,y))=0 et donc j'a...
- 07 Déc 2016, 14:56
- Forum: ✯✎ Supérieur
- Sujet: appliquer newton-raphson
- Réponses: 4
- Vues: 531
Re: appliquer newton-raphson
Merci pour la réponse. Vous avez raison, il n'y a pas de solution unique bien évidement  . Je me dirige donc vers un problème d'optimisation où l'objectif est de minimiser
. Je me dirige donc vers un problème d'optimisation où l'objectif est de minimiser ) . Grâce à l'algo du Simplex et Matlab, ça se fait tout seul
. Grâce à l'algo du Simplex et Matlab, ça se fait tout seul  .
.
- 07 Déc 2016, 13:03
- Forum: ✯✎ Supérieur
- Sujet: appliquer newton-raphson
- Réponses: 4
- Vues: 531
appliquer newton-raphson
bonjour, J'ai une fonction f qui dépend de deux variables x\in R et y\in R . Je cherche la solution tel que f(x,y)=0 numériquement. J'essaye d'appliquer la méthode de Newton-Raphson comme suit: Je pose \[X = \left[ {\begin{array}{*{20}{c}}x\\y\end{array}} \right]\] et je cherche à résoudre \...
- 07 Déc 2016, 11:41
- Forum: ✯✎ Supérieur
- Sujet: appliquer newton-raphson
- Réponses: 4
- Vues: 531
différence changement de base /de repère
Bonjour, Y a-t-il une différence entre le changement de base et le changement de repère? En effet, je possède un repère R0 et un repère R1 obtenu par une translation 3D. Je peux écrire alors que [X,Y,Z]_R0= Trans(dx,dy,dz)*[X,Y,Z]_R1 pour dire que n'importe quel vecteur dans R1 je possède son expres...
- 15 Déc 2015, 16:43
- Forum: ✯✎ Supérieur
- Sujet: différence changement de base /de repère
- Réponses: 1
- Vues: 400
Robot a écrit:Je comprends ce que tu veux, dire, mais c'est mal exprimé et ça prête à confusion.
Tu veux sans doute dire que X et X' sont les coordonnées d'un même vecteur, X étant ses coordonnées dans la base Rg et X' ses coordonnées dans la base Rt ?
Tout à fait
- 27 Nov 2015, 15:30
- Forum: ✯✎ Supérieur
- Sujet: matrice de passage: décomposition en rotations
- Réponses: 7
- Vues: 1573
1) Rg et Rt ne sont pas des matrices, juste une notation de mes bases. J'aurais dû écrire que j'ai formé une matrice tel que pour un vecteur X dans Rg et X'dans Rt , on a X=M*X'. 2) d'accord pour la définition, c'est ce que j'ai utilisé pour calculer ma matrice M: ses colonnes sont les coordonnées d...
- 27 Nov 2015, 15:22
- Forum: ✯✎ Supérieur
- Sujet: matrice de passage: décomposition en rotations
- Réponses: 7
- Vues: 1573
Merci pour votre réponse. Vous avez bien compris mon but. Cependant, j'ai fait quelques vérifications et j'ai bien la chose suivante: si M est la matrice de passage de Rg à Rt alors on peut écrire: Rg=M*Rt, y'a-t-il une incompréhension ou une convention de calcul qui change? Autrement pour vos expli...
- 27 Nov 2015, 13:58
- Forum: ✯✎ Supérieur
- Sujet: matrice de passage: décomposition en rotations
- Réponses: 7
- Vues: 1573
matrice de passage: décomposition en rotations
Bonjour, Je possède deux bases Rg et Rt. Pour calculer la matrice de passage de Rg à Rt, je calcule les vecteurs de la base de Rt dans Rg puis forme M une matrice 3*3, tel que Rg=M*Rt. De façon à calculer l'orientation de Rt par rapport à Rg, je décompose M en produit de 3 matrices de rotation selon...
- 27 Nov 2015, 11:10
- Forum: ✯✎ Supérieur
- Sujet: matrice de passage: décomposition en rotations
- Réponses: 7
- Vues: 1573
Bonjour, J'ai trouver une moyenne de 40,37 et un écart type de 2207,8891. d'abord le manque de précision dans le fait que 9% de la population soit agée de 75 et plus va changer ta moyenne et ton écart-type selon que tu considères que les 9% ont tous 75 ou bien ont tous 100 ans (un max je présume). ...
- 21 Avr 2015, 14:58
- Forum: ✯✎ Supérieur
- Sujet: Statistiques.
- Réponses: 1
- Vues: 348
suite d'éléments conjugués
bonjour, je n'arrive pas à très bien comprendre cette affirmation: " Supposons que {pk} est une suite de n directions conjuguées deux à deux. Alors les {pk} forment une base de Rn, ainsi la solution x* de Ax= b dans cette base est x_* = \sum^{n}_{i=1} \alpha_i p_i . " Normalement par la dé...
- 21 Avr 2015, 14:21
- Forum: ✯✎ Supérieur
- Sujet: suite d'éléments conjugués
- Réponses: 0
- Vues: 448
remplace Ax et Ay par leurs valeurs dans une des équations de plan merci pour la réponse mais ce qui me pose encore un problème c'est que je veux remplacer dans les 2 équations et cela donne deux Az différent! c'est plus logique de faire comme ça car le point que je cherche appartient aux 2 plans e...
- 13 Mar 2015, 09:27
- Forum: ✎✎ Lycée
- Sujet: droite dans l'espace
- Réponses: 3
- Vues: 298
- 42 résultats trouvés - Page 1 sur 3 • 1, 2, 3
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
