46 résultats trouvés
Revenir à la recherche avancée
Pythales a écrit:^2}}=...)
continue
=
-4x_n/((1+x_n)^2)})
pour obtenir le "o(zn^2) je doit faire un DL nan ?
- par mehdiphone
- 18 Jan 2015, 20:24
-
- Forum: ✯✎ Supérieur
- Sujet: aide
- Réponses: 14
- Vues: 691
zygomatique a écrit::mur:

...................
parce que le dl de sin(x)/x c'est 1-x^2/6 tu fais le produit et tu retruves ce qu'a fait manny voilà :ptdr:
- par mehdiphone
- 18 Jan 2015, 14:05
-
- Forum: ✯✎ Supérieur
- Sujet: exercice continuité
- Réponses: 25
- Vues: 967
bien vu! merci pour la 1 en étudiant la fonction on remarque que la fonction est croissante de 0 jusqu'à 1 et décroissante vers 0 donc avec une récurrence j'ai réussi à démontré cela maintenant la 2e partie me pose problème. pouvez vous détailler en m'expliquant l'aide que vous m'avez apporté? quel...
- par mehdiphone
- 18 Jan 2015, 13:38
-
- Forum: ✯✎ Supérieur
- Sujet: aide
- Réponses: 14
- Vues: 691
En étudiant la fonction \frac{2\sqrt x}{1+x} tu démontres par récurrence que x_n\in[0,1] Tu établis ensuite que z_{n+1}=\frac{1-x_n}{1+x_n}=\frac{1-x_n^2}{(1+x_n)^2} soit ... bien vu! merci pour la 1 en étudiant la fonction on remarque que la fonction est croissante de 0 jusqu'à 1 et décroi...
- par mehdiphone
- 18 Jan 2015, 13:14
-
- Forum: ✯✎ Supérieur
- Sujet: aide
- Réponses: 14
- Vues: 691

appartient ]0;1[

=(

) /(1+

) MONTRER que

appartient [0;1]
soit
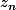
=

montrer que
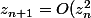)
- par mehdiphone
- 17 Jan 2015, 21:33
-
- Forum: ✯✎ Supérieur
- Sujet: aide
- Réponses: 14
- Vues: 691
mehdiphone a écrit:mince j'avais pas fait attention,

appartient ]0;1[

=(

) /(1+

} MONTRER que

appartient [0;1] et s'en suit la question de départ !
quelqu'un peut m'aider à le faire je ne comprend rien!
- par mehdiphone
- 17 Jan 2015, 21:08
-
- Forum: ✯✎ Supérieur
- Sujet: aide
- Réponses: 14
- Vues: 691
Pythales a écrit:Quelle est la relation de récurrence sur les

?
mince j'avais pas fait attention,

appartient ]0;1[

=(

) /(1+

} MONTRER que

appartient [0;1] et s'en suit la question de départ !
- par mehdiphone
- 17 Jan 2015, 20:16
-
- Forum: ✯✎ Supérieur
- Sujet: aide
- Réponses: 14
- Vues: 691
Pythales a écrit:Qu'est ce que c'est que

? C'est
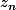
(indice) ou

?
et

? c'est
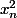
ou

?
et

? c'est
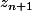
ou

ou

?
c'est
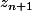
et c'est
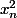
excusez moi j'ai un peu de mal.. merci
- par mehdiphone
- 17 Jan 2015, 19:26
-
- Forum: ✯✎ Supérieur
- Sujet: aide
- Réponses: 14
- Vues: 691
mehdiphone a écrit:comme je l'ai dit je commence ce chapitre et j'aimerai être familiarisé avec certains type d'exos ..
soit
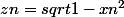
montrer que
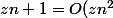)
quelqu'un peut m'aider à le faire merci
quelqu'un?
- par mehdiphone
- 17 Jan 2015, 19:10
-
- Forum: ✯✎ Supérieur
- Sujet: aide
- Réponses: 14
- Vues: 691
comme je l'ai dit je commence ce chapitre et j'aimerai être familiarisé avec certains type d'exos ..
soit
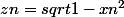
montrer que
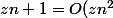)
quelqu'un peut m'aider à le faire merci
- par mehdiphone
- 17 Jan 2015, 18:27
-
- Forum: ✯✎ Supérieur
- Sujet: aide
- Réponses: 14
- Vues: 691
mehdiphone a écrit:ah je sais pas je croyais que ça ne se démontrais pas je vais essayer
je n'y arrive vous pouvez me montrer svp?
- par mehdiphone
- 16 Jan 2015, 19:00
-
- Forum: ✯✎ Supérieur
- Sujet: aide colle
- Réponses: 26
- Vues: 1789
Luc a écrit:oui c'est équivalent , mais pourquoi la deuxième ligne est-elle vraie?
ah je sais pas je croyais que ça ne se démontrais pas je vais essayer
- par mehdiphone
- 16 Jan 2015, 18:48
-
- Forum: ✯✎ Supérieur
- Sujet: aide colle
- Réponses: 26
- Vues: 1789
Luc a écrit:c'est ce que tu veux montrer ou ce que tu supposes? parce que là rien n'est démontré.
bah c'est pas équivalent?
- par mehdiphone
- 16 Jan 2015, 18:46
-
- Forum: ✯✎ Supérieur
- Sujet: aide colle
- Réponses: 26
- Vues: 1789
Dans le cadre de la topologie des espaces métriques. Sur R d(xy)=|x-y| , on dispose du théorème suivant:toute fonction continue sur un compact [a; b] est uniformément continue sur [a; b]. pour démontrer ce résultat fondamental, il faut déjà écrire correctement la définition de l'uniforme co...
- par mehdiphone
- 16 Jan 2015, 18:41
-
- Forum: ✯✎ Supérieur
- Sujet: aide colle
- Réponses: 26
- Vues: 1789
oui! ça a l'air correct. comment justifies-tu l' inégalité |\sqrt x -\sqrt y|\leq \sqrt {|x-y|} ? |\sqrt x -\sqrt y|\leq \sqrt {|x-y|} donc on a: x+y-2 \sqrt {xy}\leq |x-y| et je fais le cas x\geq y et on a 2y\leq 2\sqrt {xy} donc il existe epsilon \ |x-y|\leq \epsilon^2 \Longrightarrow |\sqrt x -\...
- par mehdiphone
- 16 Jan 2015, 18:36
-
- Forum: ✯✎ Supérieur
- Sujet: aide colle
- Réponses: 26
- Vues: 1789
oui elle l'est je pense on peut pas faire |\sqrt x -\sqrt y|\leq \sqrt {|x-y|} donc on a: x+y-2 \sqrt {xy}\leq |x-y| et je fais le cas x\geq y et on a 2y\leq 2\sqrt {xy} donc il existe epsilon \ |x-y|\leq \epsilon^2 \Longrightarrow |\sqrt x -\sqrt y|\leq \sqrt {|x-y|}\leq \sqrt {\epsilon ^2}=\epsil...
- par mehdiphone
- 16 Jan 2015, 18:17
-
- Forum: ✯✎ Supérieur
- Sujet: aide colle
- Réponses: 26
- Vues: 1789
[quote="mehdiphone"]euh non j'ai vraiment du mal sur ce chapitre que j'ai en colle mardi prochain ..... pourquoi un dessin?
- par mehdiphone
- 16 Jan 2015, 17:58
-
- Forum: ✯✎ Supérieur
- Sujet: aide colle
- Réponses: 26
- Vues: 1789
Luc a écrit:et non...
par contre, elle est uniformément continue (c'est le but de l'exercice de le monter).
Tu as fait un dessin?
Luc
euh non ? mais ce que j'ai fait est ce correcte ? merci
- par mehdiphone
- 16 Jan 2015, 17:57
-
- Forum: ✯✎ Supérieur
- Sujet: aide colle
- Réponses: 26
- Vues: 1789
mathelot a écrit:bonjour,
tu peux utiliser le DL de th() ou bien, mieux, pour faire travailler la mémoire,
retrouver le DL(0) de th(() en développant

au
voisinage de zéro
ok allons y pour le dl de th(x) dès que je le fais je l'utilise comment (je suis novice désolé) ^^
- par mehdiphone
- 16 Jan 2015, 17:29
-
- Forum: ✯✎ Supérieur
- Sujet: exercice limite thx
- Réponses: 4
- Vues: 589
continue
...................
appartient ]0;1[
=(
) /(1+
} MONTRER que
appartient [0;1] et s'en suit la question de départ !
?
? C'est
(indice) ou
?
? c'est
ou
?
? c'est
ou
ou
?
montrer que
au