20 résultats trouvés
Revenir à la recherche avancée
aymanemaysae a écrit:(a^2 + b^2)(c^2 + d^2) = a^2 c^2 + a^2 d^2 + b^2 c^2 + b^2 d^2 = (a^2 c^2 + b^2 d^2) + (a^2 d^2 + b^2 c^2)
= (a^2 c^2 + b^2 d^2 + 2 abcd) + (a^2 d^2 + b^2 c^2 - 2 abcd) = (ac + bd)^2 +(ad - bc)^2
ok merci je comprend mieux maintenant quand on a égalité avec +2abcd et -2abcd
- par Eskoris
- 12 Nov 2015, 17:04
-
- Forum: ✯✎ Supérieur
- Sujet: montrer que(a²+b²)(c²+d²) est somme de 2 carrés
- Réponses: 15
- Vues: 1715
Eskoris a écrit:Salut,

Comment on résout cette limite ? J'ai déjà calculé y = lim(x->+inf) sqrt(x) = + inf
D'où lim(y->+inf) y*exp(-y) = FI
lim(y->+inf) y/exp(y) = 0 ?
- par Eskoris
- 03 Oct 2015, 14:29
-
- Forum: ✯✎ Supérieur
- Sujet: Une autre limite
- Réponses: 1
- Vues: 233
Salut,

Comment on résout cette limite ? J'ai déjà calculé y = lim(x->+inf) sqrt(x) = + inf
D'où lim(y->+inf) y*exp(-y) = FI
- par Eskoris
- 03 Oct 2015, 14:19
-
- Forum: ✯✎ Supérieur
- Sujet: Une autre limite
- Réponses: 1
- Vues: 233
Bien sure c'est lim (x->1) (ln(x)-ln(1))/x-1 Du coup ça donne lim(h->0) (ln(1+h))/h = FI je ne comprend pas Je ne vois pas où se trouve le nombre dérivé de la fonction ln en 1 dans la proposition OK c'est bon j'ai rien dit j'ai juste pas dit que lim(h->0) ((ln(1+h)-ln(1))/h = ln'(1) = 1/1 = 1
- par Eskoris
- 03 Oct 2015, 14:05
-
- Forum: ✯✎ Supérieur
- Sujet: Une incompréhension sur la limite
- Réponses: 4
- Vues: 342
Doraki a écrit:Est-ce que tu connais la définition du nombre dérivé de la fonction ln en 1 ?
Bien sure c'est lim (x->1) (ln(x)-ln(1))/x-1
Du coup ça donne lim(h->0) (ln(1+h))/h = FI je ne comprend pas
Je ne vois pas où se trouve le nombre dérivé de la fonction ln en 1 dans la proposition
- par Eskoris
- 03 Oct 2015, 13:55
-
- Forum: ✯✎ Supérieur
- Sujet: Une incompréhension sur la limite
- Réponses: 4
- Vues: 342
Bonjour,

Je ne comprend pas pourquoi la limite est 1 alors que Y -> 0.
Pour moi on est face à une forme indéterminée à nouveau puisque le dénominateur s'annule en 0.
Quelqu'un pourrait-il me l'expliquer ?
Merci !
- par Eskoris
- 02 Oct 2015, 23:01
-
- Forum: ✯✎ Supérieur
- Sujet: Une incompréhension sur la limite
- Réponses: 4
- Vues: 342
fatal_error a écrit:salut,
suite série géométrique

sauf erreur
Merci, pourquoi je n'y ai pas pensé plus tôt ! :id:
- par Eskoris
- 12 Sep 2015, 19:52
-
- Forum: ✯✎ Supérieur
- Sujet: Une autre question
- Réponses: 2
- Vues: 322
zygomatique a écrit:salut
le conjugué d'un nombre complexe de module 1 est son inverse ... et réciproquement ...
:lol3:
et un complexe de module 1 n'est évidemment pas 0 ...
Evidement c'est plus simple comme ça... :ptdr:
- par Eskoris
- 12 Sep 2015, 19:02
-
- Forum: ✯✎ Supérieur
- Sujet: Une question de math
- Réponses: 2
- Vues: 327
Bonjour, J'ai exactement 1 question qui me pose problème : Soit \omega tel que \left | \omega \right | = 1 . Montrer que : \omega^{4}+\omega^{3}+\omega^{2}+\omega + 1 = \omega^{2} ((\omega + \bar{\omega})^ {2} + \omega + \bar{\omega} -1) Je suppose que je vais montrer l'égalité en ut...
- par Eskoris
- 12 Sep 2015, 18:14
-
- Forum: ✯✎ Supérieur
- Sujet: Une question de math
- Réponses: 2
- Vues: 327
Merci,
Je vois claire maintenant :
j^3=1
1+j=-j²
On doit montrer que (1+j)^100 = j²
Donc :
(1+j)^100 = (-j²)^100 = -j^200 = j²*(j^3)^66 = j²*1^66 = j²*1 = j²
Je fais exprès de décomposer autant...
Merci en tout cas
- par Eskoris
- 10 Sep 2015, 15:23
-
- Forum: ✯✎ Supérieur
- Sujet: (1+j)^100 = j²
- Réponses: 5
- Vues: 472
Bonjour,
Comment montrer que (1+j)^100 = j²
J'ai montré que (1+j) = -j²
Qu'est-ce qu'il faudrait faire ensuite ?
Merci
- par Eskoris
- 10 Sep 2015, 12:43
-
- Forum: ✯✎ Supérieur
- Sujet: (1+j)^100 = j²
- Réponses: 5
- Vues: 472
[FONT=Times New Roman][CENTER]Bonjour, [/CENTER] Je reviens vers vous une nouvelle fois car j'ai un petit soucis dans mon exercice de cours de mathématiques, en effet, je ne comprends pas très bien les questions et je ne sais comment y répondre... PS : L'image met quelques secondes a s'afficher [/F...
- par Eskoris
- 30 Oct 2014, 12:22
-
- Forum: ✎✎ Lycée
- Sujet: Suites numériques Terminale ES
- Réponses: 5
- Vues: 676
Donc pour le moment sigma ( 2^{p-1} ) = 1+2+4+...+ 2^{p-1} (J'ai pas précisé mais je suis en Terminal S) Je crois que j'ai trouvé. A = 2^{p-1} ( 2^p-1 ) On doit prouver que sigma (A) = 2A On a sigma ( 2^{p-1} ) = 1+2+4,...+ 2^{p-1} Et sigma ( 2^p-1 ) = 1+ 2^p-1 Donc sigma (A) = (1 + 2 + 2² +
+ 2^{...
- par Eskoris
- 30 Oct 2014, 12:08
-
- Forum: ✎✎ Lycée
- Sujet: "Exercice de TD, L2 Math-info" p 489 (Math Repère - Hachette
- Réponses: 3
- Vues: 1296
Monsieur23 a écrit:Aloha,
2^(p-1) n'est pas premier (sauf si p=1), puisqu'il est divisible par 2.
D'ailleurs, ses diviseurs sont 2;), 2¹, 2²,2³,
,2^(p-1)
Donc pour le moment sigma (
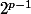
) = 1+2+4+...+
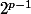
- par Eskoris
- 30 Oct 2014, 11:18
-
- Forum: ✎✎ Lycée
- Sujet: "Exercice de TD, L2 Math-info" p 489 (Math Repère - Hachette
- Réponses: 3
- Vues: 1296
Bonjour/Bonsoir, Je cherche à résoudre les questions a et b. n, un entier naturel non nul On note, sigma (n) la somme des diviseurs positifs de n. Soit p, un nombre premier tel que 2^p-1 soit premier. On note A = 2^{p-1} (2^p -1) a) Calculer sigma ( 2^{p-1} ) puis sigma ( (2^p-1) ) b...
- par Eskoris
- 29 Oct 2014, 19:52
-
- Forum: ✎✎ Lycée
- Sujet: "Exercice de TD, L2 Math-info" p 489 (Math Repère - Hachette
- Réponses: 3
- Vues: 1296
