Forum de Mathématiques: Maths-Forum

j ai pas trouvé beaucoup de résultats
sans exemples et exercices corrigés j arrive pas a comprendre la méthode

Bonjour
svp est ce que vous connaissez la methode de danilevski pour trouver le polynôme caractéristique d une matrice

Bonjour,

J'aimerais savoir comment montrer que la fonction est dérivable sur avec continue sur .

Merci

Merci beaucoup pour votre aide
pouvez-vous m'expliquer pourquoi c est une immersion

Salut Si on a \forall x \in M , il existe un voisinage u de x dans R^n un voisinage v de 0 dans R^p et une application f:V\rightarrow R^n de classe C^k tel que f(0)=x , f est une immersion en 0 et f soit un homéomorphisme de V sur alors M est une sous variété de R^n de dimension p et de classe C^k

Bonsoir à tous, j ai un problème et j'aurai besoin de votre aide s'il vous plait la question : Il faut montrer que la sphère S^n= { (x^0,...,x^n) \in R^{n+1} \ (x^0)^2 +...+ (x^n)^2 = 1 } est une sous variété de R^{n+1} par paramétrage je ne sais pas comment choisir l applica...

Mercii

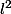
après il y a une question est ce que M dense dans c est pour ca je veux utiliser la continuité de et sa linéarité nous donne la réponse de la première question
le noyau d une fonction linéaire est un sous espace vectoriel

montrer que M est un sous espace vectoriel de l^2
montrer que M n est pas fermé

Bonjour
la suite u est dans et vaut l infinie
mais je suis désolé j ai pas bien compris .. est ce que je dois montrer que Im n est pas ouvert !
Merci pour votre patience

Bonsoir je veux montrer que l ensemble M=\left\{(X_k)_N\in l^2 \; \mid \sum_{k=1}^{\infty }X_k=0 \right\} n est pas fermé et je dois utiliser le fait que M est le noyau d une fonction non continue la fonction qui a (X_k)_N associé \sum_{k=1}^{\infty }X_k j ai essayé avec l absurde et...

ouii je l ai trouvé exactement Merci pour votre aide

Merci beaucoup

Bonjour J'ai besoin de votre aide pour cet exercice s'il vous plaît Soient X et Y deux variables aléatoires exponentielles indépendantes de paramètres λ et µ. On pose M = min(X, Y ) et D = |X − Y | =max(X, Y ) − min(X, Y ). Calculez P(M > a, D > b, X > Y ) pour a, b ≥ 0. j ai commencé par P(M > a; D...

excusez moi monsieur j ai beaucoup des problèmes dans cette matière et merci pour votre aide s'il vous plait pouvez vous me dire pourquoi c est une variété topologique et comment j utilise la définition pour répondre a cette question On considère la partie P de R^3 définie par : P= {(x,y,z,t,u) in R...

dans les exercices par exemple Soit l’application f : R --> R2 telle que f(t):=(t^2,t^3). L’image de f est-elle une sous variété ?
je sais que je dois utiliser la jacobienne mais je comprends pas pourquoi ?
Merci pour votre réponse

Bonjour j essaie de comprendre les sous variétés de Rn , dans mon cours j'ai cette définition On dit qu’un ensemble M ⊂ Rn est une sous-variété de Rn de dimension d si pour tout point de x de M, il existe — des voisinages U et V de x et 0 dans Rn — un difféomorphisme f : U → V ; tels que f(U ∩ M) = ...

desole mais je trouve pas le contre exemple

dans mon cours j'ai étudié qu il y a 2 cas possibles de groupe d ordre 4
les groupes de Klein dont tous les éléments sont d ordre inférieure ou égale a 2 isomorphe a Z/2Z * Z/2Z
et les groupes cycliques isomorphe Z/4Z
Merci

Bonjour
je cherche un contre exemple pour montrer qu un groupe abelien G n est pas toujours isomorphe a G\H*H
H un sous groupe de G
Merci pour votre aide