Forum de Mathématiques: Maths-Forum

Salut Cauchy, j'avais trouvé la réponse, il fallait juste passer par la fgm de la variable X! Ça donne tout naturellement une normale (a,a). J'avais passé près de 36 heures a bosser! Il me fallait juste un peu de sommeil. Merci quand même!!!!;);););)

Salut, pour trouver les termes de 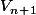, il suffit de remplacer par dans les termes de , alors le dernier terme de 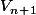sera . Bon travail.

Bjr a tous, j'ai un petit problème a vous proposer, merci déjà pour votre aide. On a une variable aléatoire \varepsilon_t telle que \varepsilon_t \rightarrow N(\mu , \sigma^2) . On définit la variable X par X=a(1+\varepsilon_t), 1 \leq t \leq n Je dois déterminer l’estimateur du maxi...

emdro a écrit:Bonjour,

qui te dit qu'on sache exprimer la somme de cette série ? C'est finalement assez rare...

Bonjour Emdro, c'est une initiative que j'ai prise sous reserve de son existence. :zen:

Pythales a écrit:Peut-être un début :


qui montre au moins que la série converge.

Merci Pythales, mais j'ai deja reussi a montrer que la serie converge!

Bonjour a tous, j'ai un petit probleme dont j'aimerais que vous m'aidiez a resoudre, si bien sur vous avez du temps libre!!! Il s'agit de calculer la somme de la serie \Sigma sin(\pi \sqrt{n^2 + 1}) . J'ai pratiquement tout essaye mais j'arrive pas a touver la somme. Une indication ou la dem...

Bonjour à tous, Mon problème se pose sur l'étude d'une série de terme général U_n= \frac{cos(n\alpha)}{n}, \alpha \in \mathbb{R} j'ai voulu passer par la transformation d'Abel en posant A_n= \frac{1}{n} et B_n = cos(n\alpha) , et voilà que je n'arrive pas a trouver comment montrer qu...

chan79 a écrit:salut
coefficient multinomial, plutôt :zen:

Un grand merci a vous tous!!;);)

Bonjour à tous, Je suis nouveau sur le forum. Mon soucis: déterminer le nombre de terme qu'il y a dans (a+b+c)^n . Je sais qu'il faut développer par le binôme de newton sur la forme ((a+b)+c)^n mais arrivé à ça je bloque. De plus je sais que le résultat sera n+2Cn "combi...