Forum de Mathématiques: Maths-Forum

Robot a écrit:Alors ça n'a pas de sens. Il y a forcément une coquille.
Ne veux-tu pas copier exactement ton énoncé ? En particulier, que te demande-t-on de montrer ?

Que est une forme bilinéaire. Ca doit etre une erreur...

Robot a écrit:Moi, je dirais plutôt que f est une forme bilinéaire. Vérifie bien ton énoncé.

Non f linéaire sur E , c'est ca qui est bizarre

Bonjour , [url]http://mp.cpgedupuydelome.fr/pdf/Déterminants%20-%20Formes%20multilinéaires%20alternées.pdf[/url] J'ai un peu près le même exo que l'exercice 1 sauf que j'ai : \phi (x,y) = f(p(x),q(y)) - f(p(y),q(x)) et f linéaire sur E mais ce ...

Jer a écrit:C'est vrai et on peut le démontrer grâce au théorème des accroissements finis (bon exercice).

Merci Jer de l'aide :we: Topic clos.

Bonjour, J'ai une question à propos d'une implication : Etant donné une fonction continue et dérivable sur \mathbb{R} privé de 0. Si la fonction est prolongeable par continuité en 0 et que \lim_{x \to 0} f'(x)=l \in \mathbb{R} alors f' peut être prolongée en 0. Est-ce vrai ? En tout cas ...

zygomatique a écrit:moi pas comprendre toi ...

Si
ALORS

zygomatique a écrit:qui c'est c'est ?

Tu veux dire que l'adhérence est égale à l'ensemble ?

zygomatique a écrit:salut

ben c'est la même chose .... avec la condition 10x =< y... ce qui fait un demi-plan pour l'adhérence .... et toujours rien pour l'intérieur ....

Donc c'est bien un fermé alors.

capitaine nuggets a écrit:Salut !

Quel que soit un ensemble , :+++:

Wow, je me sens,comment dire ... :ptdr:
Mais pour le deuxième ensemble ?

Bonjour, Dans \mathbb{R}^2 avec la norme 2 , l'adhérence de \mathbb{Q} \times \mathbb{R} , c'est bien \mathbb{R}^2 ? (sachant que l'adhérence de \mathbb{Q} est \mathbb{R} ). Par contre , je ne vois pas pour l'intérieur (l'intérieur de \mathbb{Q} est vide ?) :hum: De même pour l'ensemble des (x,y...

Donc c'est bon ?

Salut, Pour que \sqrt{a_n}-\sqrt{b_n}= c , il faut prendre a_n=(c+\sqrt{b_n})^2 . Si on prend pour b_n une suite qui tend vers l'infini (par exemple b_n=n ) puis que pour a_n on prend la partie entière de (c+\sqrt{b_n})^2 , alors... alors \lim_{n \to \infty }sqrt (\lfloor(l+...

Bonsoir,

Ma question est :

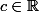
Existe t-il une suite de la forme avec tendant vers pour n'importe quel c ?

Je vois pas du tout comment construire une suite pareille tendant vers exp(1) ou ln(2) :hein:

zygomatique a écrit:ben il est évident que

i(i(x) + x) = x + i(x) donc si u = i(x) + x on a i(u) = u

et

i(i(x) - x) = x - i(x) donc si v = i(x) - x alors i(v) = -v

...

Merci :we:

Je me pose la question si F et G sont supplémentaires.
l'intersection est vide mais je n'arrive pas à montrer que F+G=E...

zygomatique a écrit:salut

énoncé incompréhensible ....

a ?
E ?
i ?

la deuxième phrase n'en est pas une (il n'y a pas de verbe dans ce qui suit la virgule)

...

J'ai édité :we:

Bonjour, J'ai un problème sur un exercice concernant les involutions. Soit E un espace vectoriel sur C; On sait que si A est un endomorphisme , nous posons F(A)= \{ x \in E / A(x)=x \} et G(A)= \{ A(x)-x / x \in E\} . F(A) et G(A) sont 2 sous espaces vectoriels. On do...

Faraziel a écrit:Bonjour,

Reprend ta factorisation, elle est fausse.

Par ailleurs je pense que c'est plus une étourderie que autre choses.

L'énoncé me donne . Xcas me donne le meme dévéloppement que le mien ....

deltab a écrit:Bonsoir.

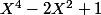
N'oublies que admet 4 racines dans et voilà tes 4 équations.

yhbvreibfuirepbfierpmbfeipm

Bonjour ,

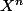
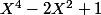
Je cherche le reste de par pour tout n.

Le polynome a 2 racines (-1 et 1) et le reste s'écrit comme un polynome de degré 3, j'ai seulement 2 équations.

Comment puis-je faire ? :hein: