Forum de Mathématiques: Maths-Forum

Bonjour,
J'aurais aimé savoir comment faire pour monter que les sous groupes finis de SL2(C) sont cyclique.
Merci d'avance,

Merci pour vos réponses !
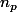
En me basant sur le 3e théorème de Sylow, on aurait , soit donc le nombre cherché ; on a et , d'où ?
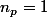
Merci encore d'avance !

Bonjour,
J'ai une question d'algèbre que j'imagine assez simple mais que je n'arrive pas à résoudre :
combien d'éléments d'ordre 5 y a t'il dans un groupe d'orde 20 ?

Merci d'avance !

Super, encore merci !

Ok ok, merci beaucoup Ben314 !
Effectivement on comprend mieux ainsi !

Bonjour, Je ne comprend pas le raisonnement suivant tenu par un de mes professeur dernièrement : H={id4 , (1,2)(3,4) , (1,3)(2,4) , (1,4)(2,3)} est un sous groupe du groupe Alterné A_4 . H\{id4} est une classe de conjugaison. Aussi H est il distingué dans A_4 et dans S_4 . Je ne comprend pas l'argum...

Bonjour, Pouriez vous m'aider à comprendre l'énoncé suivant ? : Les classes de conjugaison d'un groupe symétrique sont composées de produits de cycles à supports disjoints de même structure. Ceci signifie que le nombre de cycles de même longueur est le même pour chaque élément d'une classe de conjug...

Ok, la réponse doit donc être non.
Mais dans ton exemple, la matrice est alors déjà sous la forme recherché.

Merci pour ta réponse !

Merci pour vos réponses! Ok, désolé, mes termes étaient vraiment hasardeux. Ce que je voulais dire, c'est, si on a une matrice de la forme \begin{bmatrix}A&B\\B&A\end{bmatrix} , peut on toujours la mettre sous la forme \begin{bmatrix}D&0\\0&E\end{bmatrix} (de la même manière qu'une m...

Bonsoir,

Est il vrai qu'une matrice symétrique par bloc est diagonalisable par bloc ?
Et si oui, y a t il une méthode pour la diagonaliser en ne travaillant qu'avec les blocs ?

Merci d'avance !

Ok, je commence à comprendre, merci ! Je pense qu'il faut tout faire à la main. Si j'ai bien compris : pour trouver la solution homogène je cherche donc à diagonaliser A. Alors, avec les conditions initiales (et en ajoutant une solution particulière ( Y_p=\begin{bmatrix}\frac{1}{2}\\0\end{bmatrix} c...

Merci pour ta réponse !
Malheureusement j'ai oublié le mot le plus important dans l’énoncé !
Il s'agite de montrer qu'il existe une unique solution maximale de ce problème qui vérifie les conditions initiales qu'elle est définie sur R .
Désolé pour la coquille, et merci d'avance !

Bonjour, On me demande dans un exercice de montrer qu'il existe une unique solution (édit: maximale ) de ce problème qui vérifie x(0)=x_0 et x'(0)=0 , et qu'elle est définie sur \mathsbb{R} . Voici le problème en question : Soit \lambda > 0 et \mu > 0 , x''(t)=\la...

Bonjour, J'aurais besoin que quelqu'un me confirme (ou m'infirme) que mon implication suivante tient la route : (f_n)_n \in \ell^\infty(A,\mathbb{R}), \, \forall x \in A, \forall \epsilon >0, \exists N \in \mathbb{N}, \forall n > N, |f_n(x)-f(x)|<\epsilon implique \fo...

Parfait, merci à vous !

Merci pour vos réponses ! :) Comme dit, je pensais utiliser le théorème de convergence dominé en disant \| f_n \|_2 \leq \sqrt(C) , X étant de mesure finie, \sqrt(C) est intégrable. On peut alors intervertir limite et intégrale et utiliser la continuité de x \longmapsto x^2 (à moins ...

L'ensemble des valeurs pour les quelles fn ne tend pas vers f est des mesure nulle.

Il y a quand même quelque chose que je ne comprend pas...
Le fait que fn tende vers f p.p entraine t'il que ?

Bonjour, Je n'arrive pas à voir comment proceder pour démontrer l'inégalité suivante. Je pensais utiliser le théorème de convergence dominé, mais ça ne semble finalement pas approprié... (X, A, \mu) espace mesuré de mesure finie, (f_n)_n suite de fonctions mesurables à valeurs réel c...

Merci à tous pour votre aide :) Finalement je pense qu'il est plus sage de renoncer à vouloir s'accrocher à garder k dans Z, alors qu'une petite modification de l'énoncé rend l'exercice beaucoup plus facile. En effet si on pose a_0(x)=E(x) et a_n(x)=E(10^nx)-10E(1...