Forum de Mathématiques: Maths-Forum

Salut, je suppose que tu ne connais pas les développements limités... Pour la deuxième, il n'y pas de soucis, le numérateur tend vers 2 et le dénominateur vers 0.... Pour la troisième, remarque que x \sin \frac{3}{x} = 3 \frac{\sin \frac{3}{x}}{\frac{3}{x}} Ca devrait t'aider... Et pour la première,...

Merci de votre réponse. Je ne vais vous parler que du cas cylindrique puisque l'autre est visiblement correct. Je dispose d'une courbe Force / allongement. Le problème est qu'ici la partie linéaire de ma courbe ne passe pas par 0. La question est posée comme cela : calculer le coefficient linéaire l...

Bonjour, je dispose de 2 échantillons en aluminium. L'un est cylindrique et l'autre est de section rectangulaire. Je dois chercher les modules d'Young dans les 2 cas. Or je trouve des résultats très différents : 18 GPa pr le cylindre et 69 GPa pr la section rectangulaire. Je devrais pourtant trouver...

Bonjour, quelqu'un sait-il où je peux trouver la correction de l'épreuve d'informatique MP du concours des Mines, Ponts et Chaussées de 2006 ?
J'aimerais m'entraîner pendant les vacances et si je pouvais avoir la correction, cela m'aiderait beaucoup. Merci de votre aide.
Bonne journée.

Oui oui c'est un peu ce que j'avais dit mais c'est vrai que c'était incompréhensible. :hum:

Bonsoir.
x*ln(1+1/x) = ln(1+1/x)/(1/x) ..
Tu utilises la limite en 0 de ln(1+x)/x (après changement de variable) ;)

Oui oui bien sur autant pour moi j'avais pas bien regardé. :dodo: Par contre en effet il faut voir si on peut avoir du degré impair. ça paraît bien en soustrayant le polynome de degré le plus haut de la première famille avec le polynome de degré le plus haut de la seconde. On fait ainsi "partir" le ...

Je suis d'accord avec ce que tu as dit mais je ne comprends pas en quoi ça répond à la question. On veux que la famille soit une base et je ne vois pas du tout comment montrer que la réunion de tes 2 familles est une base de Rn[X].. Merci de m'éclairer :id: :we:

Certes c'est nécessaire mais tu crois que c'est suffisant ?
Si oui une petite idée de démo ? Parce que moi à première vue je ne vois vraiment pas. :briques:

En effet c'est quand même formidable cette découverte ! ça voudrait dire que le cos est périodique et que quand x est congru à Pi [2 Pi] , cos x = -1 et quand x est congru à 0 [2 Pi] , cos x =1 .. ?? :hum:

:ptdr: :ptdr:

Bonjour je suis en mpsi et jai besoin de votre aide pour un exo dont voici l'énoncé. Donner une condition nécessaire et suffisante sur \large n \in \mathbb{N} pour que \large \mathbb{R}_n [x] admette une base formée de polynomes sans racines réelles. Je ne vois vraiment pas quoi faire. Merci de votr...

re bonjour quelqu'un pourrait il me donner une solution svp. je me fais un peu pressant mais c'est quand même assez important. merci beaucoup.

oui simon je sais bien quil n'y a pas 50 possibilités pour obtenir 1. -1 et -1, et 1et 1. je doute que je serais en mpsi si j'ignorais cela. mais c'est très bien mais je ne comprend pas le rapport avec ma question. je veux montrer que si a+b sqrt 2 est inversible alors on a a^2-2 b^2=1\ ou\ -1 . mer...

je suis vraiment dèsolè.en génèral je n'ai pas de mal a comprendre les math mais la j'avoue que je ne vois pas le rapport avec mon sujet. je suis d'accord avec tout ce que vous me dites bien sur mais je n'arrive pas a expliciter les ... . je suis désolé. merci de me fournir une derniere explication ...

merci bruce mais c'est ca mon probleme. je ne comprend pas pourquoi cela entraine que 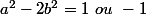. merci de votre aide.

en effet je ne sais pas ce qu'est la norme. de plus bruce je connait l'expression de l'inverse et je suis tout a fait daccord pour dire que si a-2b^2=1 ou -1 cest inversible. la ou est mon probleme en rèalitè c'est pour la dèmonstration de la rèciproque. merci de votre aide.

bonjour thsq. merci d'abord de cette reponse. cependant j'ai du mal à suivre le raisonnement. qu'est ce que N? merci

bonjour. j'ai besoin d'aide pour une démo. on considère l'anneau . sachant que Z[sqrt2] est l'ensemble des 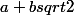avec 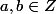. Je voudrais montrer que l'ensemble des éléments inversibles de l'anneau est tel que 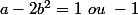. merci de votre aide.

Re bonsoir quelqu un pourrait il me fournir une explication ? merci et bonne soirée.

excuse moi yos mais en redigeant l'exercice je ne rends compte que je n'ai pas si bien compris que ça. on a donc si j'ai bien compris le début : dZ est un sous groupe de Z avec n|d. mais en fait je ne vois pas le rapport avec les sous groupes de Z/nZ. je me doute que c'est sûrement bête mais je croi...