Forum de Mathématiques: Maths-Forum

il faut faire la différence entre les constantes et le reste. Quand tu dérives la fonction f, 2 à la puissance n est une constante (ne dépend pas de x), le cos lui dépend de x, on peut écrire f^(n) (x) = 2^n cos(g(x)) avec g la fonction qui à x associe 2x + npi/2,

non, 0... f est constante : pour tt x, f(x) vaut la même chose

Dwarfs43 a écrit:Voilà je suis de retour, et j'ai pas compris mon erreur, il faut bien que je dérive

Si f est définie par : , quelle est la dérivée de f ?

non ! La dérivée est fausse : tu dérives en fonction de x, pas de n !

excuse moi, j'ai oublié le 2 devant le x précédemment, et tu as du coup fait pareil
C'est une fonction dont x est la variable, n est une constante, 2 puissance n aussi...

Bin je dois prouver que la dérivé de : 2^n cos(x+n\frac{\pi}{2}) 2^{n+1} cos(x+n+1\frac{\pi}{2}) attention à l'utilisation de ce genre de symbole, ça ne veut rien dire... Mais je crois que tu as quand même compris, tu sais dériver une composée ? (attention aux parenthèses dans le cos)

En fait P(n) c'est la propriété "pour tt x bla bla bla". Tu peux pas dériver ça ! Mais tu supposes P(n) c'est à dire, tu dis : Supposons que pour tt x , f^{(n)}(x) = 2^n cos(x + n\frac{\pi}{2}) Et après tu veux déduire P(n+1), tu peux me dire ce qu'est la propriété ...

bah f c'est la fonction au départ, tu la dérives n fois et tu veux savoir ce que ça donne.
Ensuite le raisonnement pour l'hérédité est toujours le même : tu supposes P(n) et tu montres P(n+1).
Je t'ai donné P(n), qu'est-ce que c'est P(n+1) ? Comment le prouver ?

Exactement, alors par récurrence on veut montrer pour tout : pour tt de . Qu'est-ce qui te bloque ?

ok, donc l'initialisation est faite ?
C'est quoi la dérivée (n+1)ème d'une fonction ? (en fonction de la dérivée nième)

et pourquoi pas une récurrence ?

Non ce n'est pas stable : si tu prends 6 = 4*1 + 2 et 2 = 4*0 + 2, 6*2 = 12 = 4*3 + 0 n'est pas dans l'ensemble

pas de souci, tu as tout compris ? Tu as fait l'autre ?

Pas besoin de récurrence pour 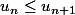, comme on a étudié f, on peut voir que est positif sur, car si on a montré que est dans cet intervalle pour tout n, l'est aussi.

C'est pas grave :) Alors si j'ai a dans C et b dans C par exemple, il existe l tel que a = 4l+1 , et il existe m tel que b = 4m+1 , alors soient de tels l et m . ab = (4l+1)(4m+1) = 4*(4lm) + 4l + 4m + 1 = 4(4lm + l + m) + 1 . On pose k = 4lm + l + m , k est bien un e...

Il faut vérifier si A est stable par multiplication ? Et si C l'est ? Si c'est ça la question est : si je multiplie entre eux deux éléments de A, le résultat est-il dans A ?
Au fait k2 c'est k au carré ?

Attention, s n'est pas la fonction qui à x associe \frac{(-1)^n}{n!(n+x)} , mais qui associe la série de terme général u_n = \frac{(-1)^n}{n!(n+x)} . Il s'agit pour montrer que s est bien définie de prouver l'existence et la convergence de cette série pour x\in\mathbb...

zygomatique a écrit:le produit d'un rationnel par un irrationnel est irrationnel sauf quand ce rationnel est 0

C'est vrai et c'est l'argument à utiliser

un rationnel est irrationnel si et seulement si il est nul .... Je ne suis pas d'accord. 0 = \frac{0}{1} est rationnel. Les irrationnels sont par définition les réels qui ne sont pas rationnels, donc 0 n'est pas irrationnel. Tu utilises le fait que le produit d'un rationnel et d'un irrationnel est ...

Il s'agit de dériver une fonction qui est le produit de deux fonctions que tu sais dériver, donc oui.
Tu obtiens quoi ?