Forum de Mathématiques: Maths-Forum

Je ne sais pas pourquoi j'ai écrit A nilpotente. J'avais juste comme hypothèse que A est carrée d'ordre n de rang 1, ce qui me donne bien A+I diagonalisable si et seulement si A l'est donc si et seulement si tr(A) n'est pas nulle. Désolée de cette grossière erreur. On a donc B(B^{-1}A+I) ave...

Bonjour, L'indication doit plutôt être: \dfrac{1}{k^2}<\dfrac{1}{k(k-1)} . Si la suite \alpha_n est majorée alors tu peux aussi majorer le terme W_n avec l'inégalité ci-dessus et en sachant que \dfrac{1}{k(k-1)}=\dfrac{1}{k-1}-\dfrac{1}{k} la somme va se s'implifier par télescopage.

Bonjour,

L'indication doit plutôt être: .
Si la suite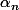 est majorée alors tu peux aussi majorer le terme 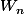avec l'inégalité ci-dessus et en sachant que

Bonjour, J'ai une matrice A carrée d'ordre n nilpotente de rang 1 et une matrice B carrée d'ordre n inversible. Je cherche une condition nécessaire et suffisante pour que A+B soit diagonalisable. J'ai fait le cas particulier B=I qui fonctionne bien: A+I est diagonalisable si et seulement si A l'est ...