Forum de Mathématiques: Maths-Forum

Ouf, me voila soulagé !

Merci :)

Bonjour à tous, je viens à vous car j'ai un petit souci mathématique. J'ai la fonction f(x)= ;)(x1+x2) dont je dois trouver le gradient. D’après mon corrigé, la réponse serait [ 1/(2*;)(x1*x2)) , 1/(2*;)(x1*x2)) ] Cependant, étant donné que la formule de dérivation de ;)(u) est u’/(2*;)(u)), je trou...

Ah oui d'accord j'ai compris.

Merci beaucoup à vous tous :)

Là, c'est niveau collège vu que la factorisation est triviale : 12x_2^2+4x_2-x_2=3x_2(4x_2-1) est nul ssi un des deux facteurs est nul. Voui, en fait pour (0,0) j'ai compris, par contre je ne vois pas du tout comment on arrive à trouver (-1/2 , -1/4) :hein: Enfin logiquement je comprends mais je ne...

Salut et merci de ta réponse

En fait je n'arrive pas du tout à comprendre comment tu trouves les deux valeurs de .

J'ai essayé de résoudre comme un polynôme du seconde degré, ce qui me donne 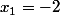et 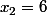mais cela est faux puisque ça ne respecte pas

Bonjour à tous, Je viens vers vous car j’ai un gros souci avec un exercice. J’ai la fonction f(x)= x1^(3) + x1^(2) – x1x2 + x2^(2) et je dois déterminer les points stationnaires de cette fonction. J’ai donc commencé par déterminer le gradient [grad f](x) = (3x1^(2) + 2x1 – x2 , -x1 + 2x2) Puis j’ai ...

Bonjour, grâce à vous j'ai compris un peu plus : q''(x) est de la forme -u'/u2 où u= 2 X ;)(x+1) = 2 X (x+1)^(1/2) d'où u'= 2 X 1/2 X (x+1)^(-1/2) Donc q''(x) = -2 X 1/2 X (x+1)^(-1/2) / [2 X ;)(x+1)]^2 Donc q''(x) = -(x+1)^(-1/2) / 4(x+1) Mais je n'arrive pas du tout à aller plus loin, pourriez-vou...

Sylviel a écrit:Regarde dans un formulaire quelconque ce que vaut la dérivée de
quand u est une fonction de x

Bonjour et merci de votre réponse

La dérivée de u est u’/(2 X u), mais q’(x) est de la forme 1/u, du coup je comprends pas pourquoi utiliser cette formule plutôt que –u’/u^2

q'(x)=\frac{(x+1)'}{2\sqrt{x+1}}=\frac{1}{2\sqrt{x+1}} q''(x)=\frac12.(-\frac{(\sqrt{x+1})'}{(\sqrt{x+1})^2})=\frac12.(-\frac{1}{2 \sqrt{x+1}}.\frac{1}{x+1})=-\frac14.\frac{1}{(x+1)\sqrt{x+1}} Bonjour à vous deux et...

Bonjour à tous, Je suis un étudiant qui rentre cette année en L2 d’économie, et n’étant pas très fort en maths j’ai profité de ces vacances pour réviser mes cours de maths. Cependant, il y a un exercice auquel je n’arrive vraiment pas à répondre, et c’est pourquoi je suis venu vous appeler à l’aide ...

Bonjour à tous !

En fait j'ai fait une erreur de frappe : l'équation était bien (a+1)y = -2a-2 et pas (a+1)a= -2a-2. Mea culpa.

Encore merci pour votre aide :)
Slataper

D'accords, j'ai compris !

Merci beaucoup ! :we:

Bonjour à tous ! :we: J’ai un petit problème avec une équation qui me perturbe. J’ai (a+1)a = -2a-2 où a est un paramètre, et je sais que le résultat est y= -2, seulement je n’arrive pas du tout à comprendre comment il faut faire pour le trouver. La seule chose que j’arrive à faire, c’est diviser l’...