Calcul limite

[Tessel75]

Bonjour,
Je voudrai savoir quelle est la valeur de :

B = (A/(2*3)) + (A/(2*5)) + (A/(2*7)) + (A/(2*9)) +(A/(2*11)) + ...... + (A/(2*ri ))

Je vous remercie de votre attention.
Je ne suis pas étudiant, juste un retraité qui se pose cette question.

[AMARI]

Bonjour,

C'est une suite géométrique de raison (1/(2*2)) .

[Ben314]

Salut,

C'est une suite géométrique de raison (1/(2*2)) .

On ne doit pas comprendre l'énoncé de la même façon vu que ce que je lit, c'est

où je suppose que est un entier naturel impair .
Si c'est bien ça, le seul vague truc qu'on peut faire, c'est d'exprimer le résultat en fonction des Nombres harmoniques dont on connait bien le comportement asymptotique :

[AMARI]

Bonjour Ben314,

Ce que j'ai compris, que c'est une puissance (1/(2*2)) (1 sur 2 puissance 2) et non une multiplication.
Merci Beaucoup Ben.

[Tessel75]

Bonjour à tous les deux, je vous remercie pour vous être attardés sur ma question.
Premièrement, je dois dire que ma question est ben celle qu'a reformulé Ben. Je n'avais vu que trop tard la possibilité d'écrire des formules; ce qui n'est pas bien malin de ma part. Pour rappel, sur le clavier on tape "*" pour "x", multiplier, et "^" pour élever à la puissance.
Cela étant dit, j'ai cliqué sur le lien des nombres harmoniques, ce qui répond tout à fait à ma question; j'ignorais le terme "nombres harmoniques". Je me pencherai donc cet après-midi sur la page Wikipédia liée. Néanmoins, permettez moi de prolonger ma question.

Qu'est ce que le et le 2n+1 - ? Et aussi, quelle est la valeur de cette asymptote, parce que j'avais bien compris que le comportement était asymptotique, et c'était bien pour ça que j'ai posé ma question sur le forum.
Et alors je voudrai aller au bout de mon interrogation en demandant comment traiter le problème si les inverses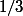 _,__,_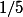 _ ,_ _ ,_ ne concernent que les nombres premiers ?

Désolé, je n'arrive pas à maitriser l'éditeur de formules.
Encore merci, je suis impatient de lire vos réponses

[vam]

Bonjour
Je ne fais que passer

pour écrire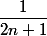 tu saisis le code \dfrac{1}{2n+1} que tu mets entre les balises

[Ben314]

La somme des inverses de nombres premiers, c'est aussi un truc classique dont on connait le comportement asymptotique :
https://fr.wikipedia.org/wiki/S%C3%A9ri ... s_premiers

[Tessel75]

Merci beaucoup ! C'est exactement la réponse que je cherchais. Encore merci, et bonne soirée.

Je repose conjointement une nouvelle question. Existe-t-il une formule qui donne le nombre de nombres premiers inférieurs une borne B ?

[Ben314]

On a des estimations asymptotiques de la fonction de décompte des nombre premiers (c'est le théorème des nombres premiers), mais c'est évidement moins précis que par exemple la somme des inverses des entiers vu que la répartition des nombres premiers est (évidement) plus chaotique . . .