Limite

[pseudodupseudo]

Bonsoir,

pouvez vous me donner un coup de pouce pour calculer la limite ci dessous. J'ai pensé aux formules d'équivalences sans resultats, changement de variable également.


j'ai pensé à dire que y=1/x²
j'ai donc:

l'équivalence de ln(1+y) en 0 est y donc la limite devient:
= +oo

Merci à vous.

[pseudodupseudo]

Personne pour de l'aide svp ?

[laetidom]

Personne pour de l'aide svp ?

Bonjour,

à la calculatrice graphique je vois que l'expression tend vers +inf quand x tend vers +inf

j'ai fait x^3((1 + (ln(1+(1/x^2)))/x^3) et :

(ln(1+(1/x^2))) tend vers 0 en +inf car ln(1)=0

donc (ln(1+(1/x^2)))/x^3) tend 0 en +inf

donc ((1 + (ln(1+(1/x^2)))/x^3) tend vers 1 en +inf

donc x^3((1 + (ln(1+(1/x^2)))/x^3) tend vers le signe de x^3 donc vers +inf quand x tend vers +inf

par contre, je ne suis pas trop sûr de moi.....

[landagama]

Cette limite n'est pas facile; il y a une formule dans ton cours qui va t'aider :

On va essayer de s'y ramener dans ta limite.
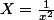
Tu as donc on va poser pour avoir qu'il va falloir diviser par X (c'est-à-dire multiplier par x^2) pour retrouver la formule du cours .

Déjà, es-tu d'accord que lorsque x tend vers +linfini, X=1/x² tend vers 0 ?

Le plus simple c'est d'écrire que :
Voici ce que cela donne quand on passe à la limite :
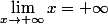
- D'abord : (évident).
- Ensuite :
(formule du cours).
- Enfin : par produit on en déduit : et voilà le travail !

As-tu compris ? Elle n'était pas du tout simple cette limite mais j'espère t'avoir aidé(e) à mieux la comprendre !

Tu peux venir voir mon blog de maths si ça te dit : http://www.bossetesmaths.com

[laetidom]

Cette limite n'est pas facile; il y a une formule dans ton cours qui va t'aider :

On va essayer de s'y ramener dans ta limite.
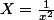
Tu as donc on va poser pour avoir qu'il va falloir diviser par X (c'est-à-dire multiplier par x^2) pour retrouver la formule du cours .

Déjà, es-tu d'accord que lorsque x tend vers +linfini, X=1/x² tend vers 0 ?

Le plus simple c'est d'écrire que :
Voici ce que cela donne quand on passe à la limite :
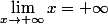
- D'abord : (évident).
- Ensuite :
(formule du cours).
- Enfin : par produit on en déduit : et voilà le travail !

As-tu compris ? Elle n'était pas du tout simple cette limite mais j'espère t'avoir aidé(e) à mieux la comprendre !

Tu peux venir voir mon blog de maths si ça te dit : http://www.bossetesmaths.com

Bonjour landagama, heureusement que j'ai dit que je n'étais pas sur !...mais je vois que tu l'a calculé en o (!?), ça n'était pas en +inf ? excusez-moi !....
-------------------------------------------------------------------
Ah je viens de voir que tu l'a modifié et que je retombe sur mes pattes, je suis content mais par contre peux tu me dire si ma démarche est correcte puisque le résultat l'est, je te remercie bien !

[pseudodupseudo]

Bonjour landagam,
vous aviez fait une erreur à la fin que vous avez corrigé.

merci j'ai tous compris votre méthode qui permet d'amener une équivalence en zéro en faisant intervenir un changement de variable avec le X=1/x²

Je vous remercie beaucoup.

[laetidom]

Bonjour landagam,
vous aviez fait une erreur à la fin que vous avez corrigé.

merci j'ai tous compris votre méthode qui permet d'amener une équivalence en zéro en faisant intervenir un changement de variable avec le X=1/x²

Je vous remercie beaucoup.

------------------------------------------


J'ai fais ce que j'ai pu ou su !!! désolé....