Inéquation avec exponentiel
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
gaalee89
- Messages: 7
- Enregistré le: 15 Jan 2014, 14:56
-
 par gaalee89 » 16 Jan 2014, 11:16
par gaalee89 » 16 Jan 2014, 11:16
Bonjour, je dois résoudre 2lnx-1>0 alors j'ai commencé mais je suis bloqué à un moment :
2lnx-1>0
2lnx>1
2lnx>lne
ln(x)2>lne
x²>e
x²-e>0
Là je fais le delta=b²-4ac
delta=0²-4x1xe
=-4xe
Qui est a peu pres =-10,8
delta<0
Donc ax²+bx+c est du signe de a ?
Et là je ne sais pas quoi écrire pour finir la démonstration de cette inéquation. Pouvez-vous me venir en aide ? Merci :)

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 16 Jan 2014, 11:51
par fatal_error » 16 Jan 2014, 11:51
slt,
Donc ax²+bx+c est du signe de a ?
a lexterieur des racines.
lautre methode, immediate:
x^2-e = (x-sqrt(e))(x+sqrt(e))
(de lidentite remarquable a^2-b^2
et apres tableau de signe.
la vie est une fête

-
gaalee89
- Messages: 7
- Enregistré le: 15 Jan 2014, 14:56
-
 par gaalee89 » 16 Jan 2014, 13:31
par gaalee89 » 16 Jan 2014, 13:31
fatal_error a écrit:slt,
a lexterieur des racines.
lautre methode, immediate:
x^2-e = (x-sqrt(e))(x+sqrt(e))
(de lidentite remarquable a^2-b^2
et apres tableau de signe.
Donc pour conclure je fais le tableau de signe alors ? Mais je ne trouve pas les solutions de linéquation.
Et pour l'utilisation de l'identité sa donnerait :
lnx²-lne²>0
(lnx-lne)(lnx+lne)>0
donc les solutions sont lnx>1 et lnx>-1 c'est bien ça ?
-
gaalee89
- Messages: 7
- Enregistré le: 15 Jan 2014, 14:56
-
 par gaalee89 » 16 Jan 2014, 19:37
par gaalee89 » 16 Jan 2014, 19:37
Excusez moi du double poste et de mon impatience mais serait-il possible d'avoir une réponse ? ^^
Merci

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 16 Jan 2014, 19:47
par fatal_error » 16 Jan 2014, 19:47
2ln(x)-1>0
<=>
ln(x)>1/2
<=>
e^(ln(x))>e^(1/2)
car e est une fonction strictement croissante et donc
x>e^(1/2)
la vie est une fête

-
Black Jack
 par Black Jack » 16 Jan 2014, 19:47
par Black Jack » 16 Jan 2014, 19:47
ln(x) n'existe que si x > 0
Donc 2.ln(x) - 1 > 0 ne doit être considéré que pour x > 0
2.ln(x) - 1 > 0
ln(x²) - 1 > 0
ln(x²) > 1
ln(x²) > ln(e) ; et comme ln(x) est strictement croissante -->
x² > e
et comme il faut aussi x > 0, les solutions sont x dans ]Racinecarrée(e) ; +oo[
:zen:
-
gaalee89
- Messages: 7
- Enregistré le: 15 Jan 2014, 14:56
-
 par gaalee89 » 16 Jan 2014, 20:38
par gaalee89 » 16 Jan 2014, 20:38
Vous me donnez tous les deux, une réponse différente laquelle dois-je croire ? ^^
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 16 Jan 2014, 20:54
par Carpate » 16 Jan 2014, 20:54
-
gaalee89
- Messages: 7
- Enregistré le: 15 Jan 2014, 14:56
-
 par gaalee89 » 16 Jan 2014, 21:11
par gaalee89 » 16 Jan 2014, 21:11
Carpate l'identité remarquable que tu as utilisé n'est pas applicable ici vu que e ne peut pas être égal à e² !
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 17 Jan 2014, 05:03
par Carpate » 17 Jan 2014, 05:03
gaalee89 a écrit:Carpate l'identité remarquable que tu as utilisée n'est pas applicable ici vu que e ne peut pas être égal à e² !
e n'est pas égal à
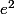
mais à
^2)
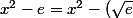^2=(x-\sqrt{e})(x+\sqrt{e}))
-
Black Jack
 par Black Jack » 17 Jan 2014, 11:25
par Black Jack » 17 Jan 2014, 11:25
gaalee89 a écrit:Vous me donnez tous les deux, une réponse différente laquelle dois-je croire ? ^^
Celle que tu veux, les 2 réponses sont équivalentes contrairement à ce que tu penses.
:zen:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 90 invités
